Вписанные углы и счёт углов в окружности
Ошибка.
Попробуйте повторить позже
В треугольнике провели высоты
и
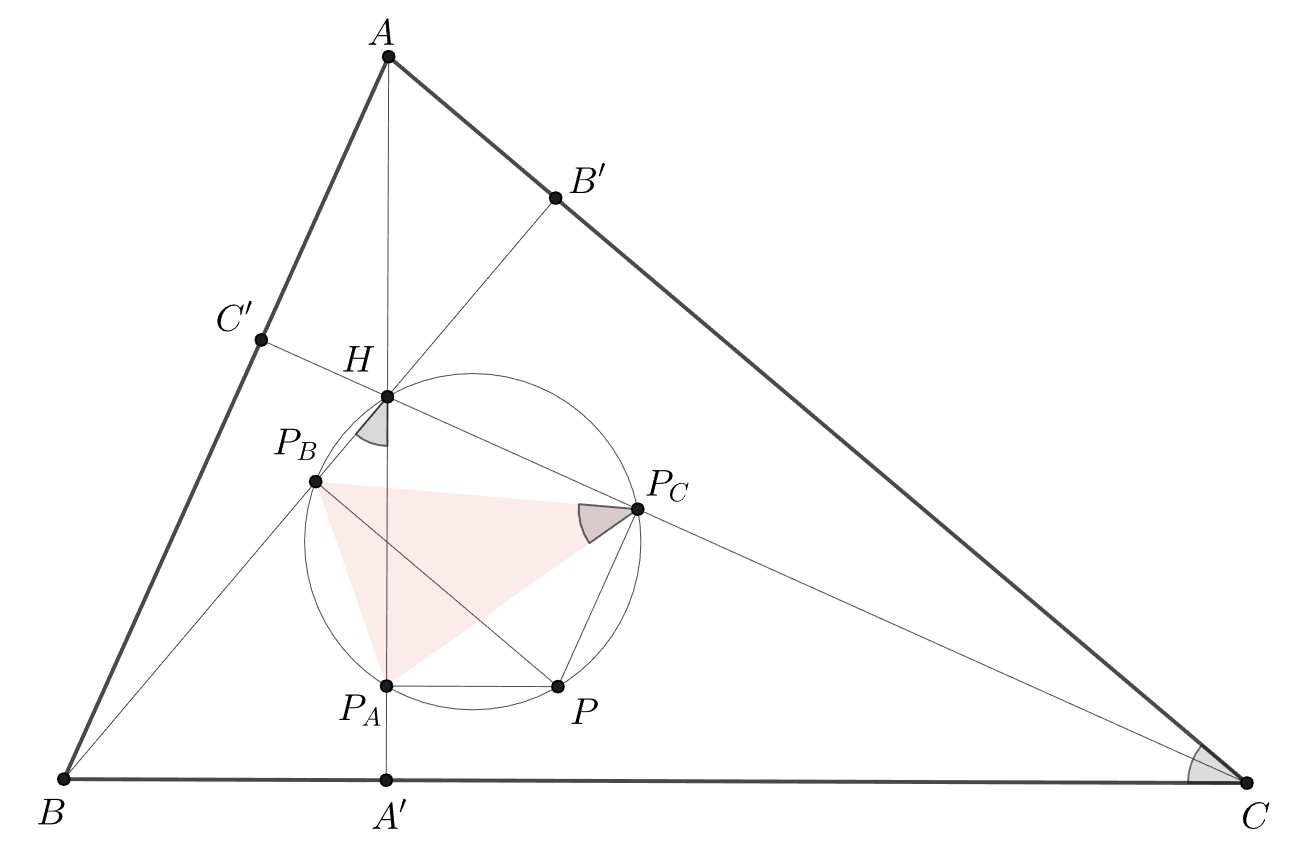
(a) Точку спроектировали на высоты треугольника. Докажите, что треугольник, для которого эти три проекции являются
вершинами, подобен треугольнику
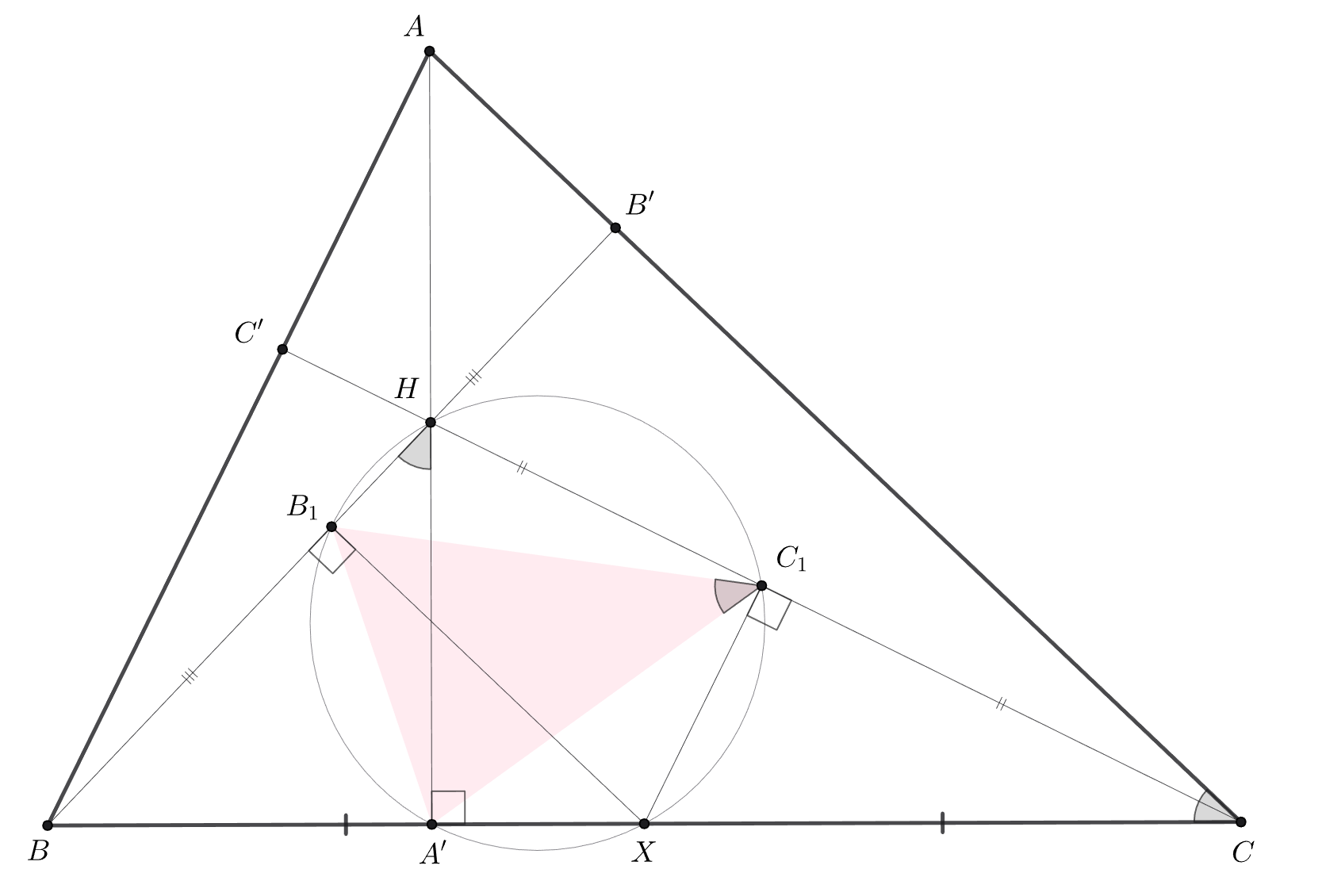
(b) Пусть — середины высот
и
Докажите, что треугольники
и
подобны.
(c) На высотах взяли точки так, что они делят высоты в отношении
считая от вершины. Докажите, что
треугольники
и
подобны.
Подсказка 1
Давайте вспомним факт про 5 точек на окружности. Пусть есть три прямые, пересекающиеся в точке X. Если взять некоторую точку P и провести из неë перпендикуляры к прямым, то основания перпендикуляров, P, X, лежат на одной окружности.
Подсказка 2
Во втором и третьем пунктах нужно найти, в какой точке пересекаются перпендикуляры, проведëнные к высотам в точках, указанных в условие, тогда получится применить факт. Как же найти? Проведите перпендикуляр к высоте и поищите какую-то особенную точку в треугольнике, через которую он проходит.
(a) Обозначим проекции через и
а ортоцентр
через
Заметим, что пятиугольник
вписанный.
Далее просто перекинем углы:
Аналогично получим другие равенства углов, которые влекут подобие.
(b) Пусть — середина
— ортоцентр. Заметим, что точки
лежат на одной окружности, потому что
Далее аналогично предыдущему пункту перекидываем углы:
(c) Давайте к каждой высоте проведём в точках прямые, перпендикулярные им. Если докажем, что они пересекаются в
одной точке, то решение сведётся к первому пункту. А это действительно так, потому что они пересекаются в точке пересечения медиан (это
следует из того, что точка пересечения медиан делит медиану в отношении
к
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




