Касание с окружностью и касание окружностей
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник около которого описана окружность
и в котором проведены высоты
Касательные к
проведенные в точках
и
пересекаются в точке
и прямая
пересекает прямые
в точках
соответственно. Докажите, что описанная окружность треугольника
касается
Источники:
Подсказка 1
Нас просят доказать, что окружность (ABC) является полувписанной окружностью треугольника DEF. Существует лемма Верьера, которая утверждает, что если окружность касается двух сторон треугольника и прямая, содержащая точки касания, содержит его инцентр, то такая окружность является полувписанной.
Подсказка 2
Чтобы подогнать задачу под эту лемму, достаточно поперекидывать углы и показать, что FI и EI — биссектрисы.
Подсказка 3:
По-хорошему саму лемму тоже надо бы доказать. Для этого нужно вспомнить лемму Архимеда и рассмотреть радикальную ось некоторой точки и окружности.
Пусть — основание высоты
проведенной из точки
а
— середина
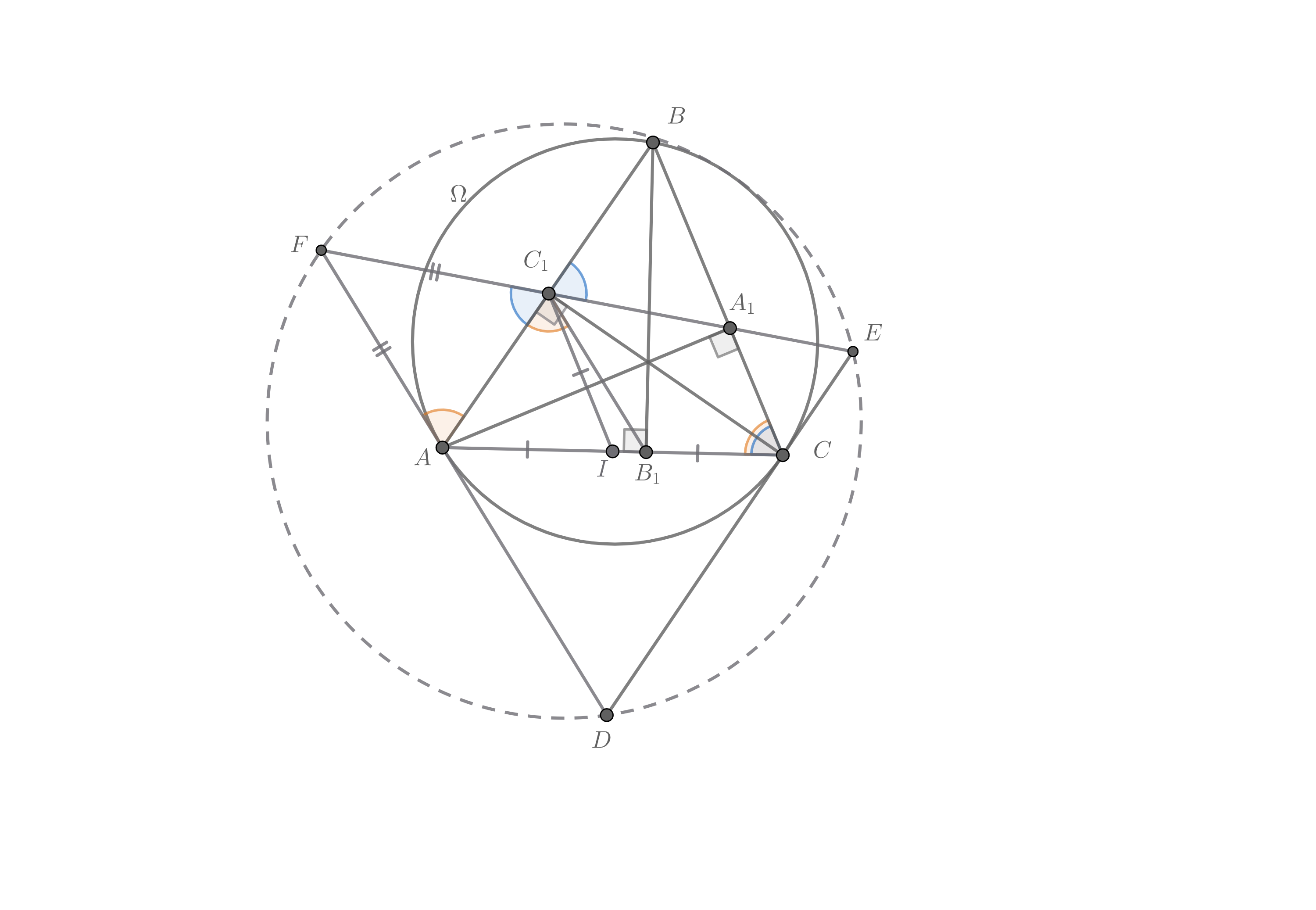
Заметим, что
откуда аналогично и
Тогда можно записать такую цепочку равенств:
Откуда следует Ввиду
имеем
Из равенства треугольников следует, что
–
биссектриса угла
Аналогично получаем, что
– биссектриса угла
т.е.
– центр вписанной окружности
Вспомним одно утверждение: отрезок, соединяющий точки касания полувписанной окружности треугольника с его сторонами, содержит центр вписанной окружности этого треугольника. Очевидно, верно и обратное: если окружность касается двух сторон треугольника так, что отрезок, соединяющий точки касания, содержит центр вписанной окружности этого треугольника, то первая окружность является полувписанной (т.е. касается двух сторон треугольника и его описанной окружности).
В нашей задаче окружность касается сторон треугольника
в точках
причем отрезок
как было доказано ранее,
содержит центр
вписанной окружности треугольника
— значит,
является полувписанной окружностью треугольника
т.е. касается его описанной окружности, что и требовалось доказать.
Теперь докажем использованное утверждение, называемое леммой Веррьера:
Лемма (Веррьера). Окружность касается сторон
треугольника
в точках
соответственно и касается
внутренним образом описанной окружности в точке
Докажите, что инцентр (центр вписанной окружности)
треугольника
лежит на прямой
Заметим, что по лемме Архимеда прямая проходит через середину дуги
описанной окружности, не содержащей точку
Аналогично, прямая
проходит через середину дуги
не содержащей вершину
Обозначим середины этих дуг через
соответственно.
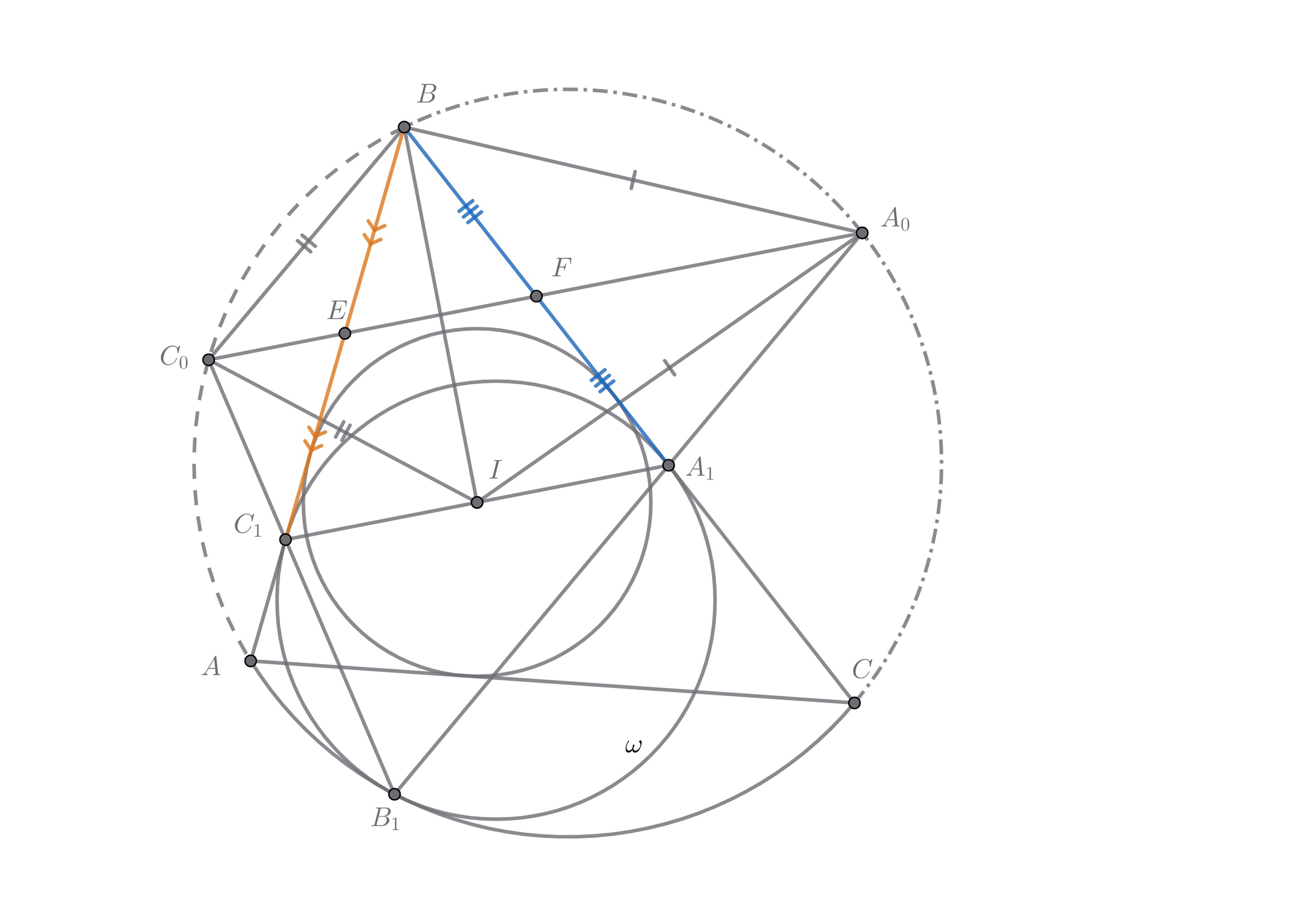
Из той же леммы Архимеда следует, что Следовательно, степень точки
одинакова относительно окружности
и точки
Аналогичное утверждение верно и для точки
Из этого следует, что прямая
— радикальная ось точки
и
окружности
Поэтому прямая
проходит через середины отрезков
Значит, прямая
содержит среднюю линию
треугольника
Следовательно, образ точки
при отражении точки
относительно прямой
лежит на прямой
С другой стороны, по лемме о трезубце и
Поэтому точка
при отражении относительно прямой
переходит в точку
Откуда и следует, что точка
лежит на прямой
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




