Касание с окружностью и касание окружностей

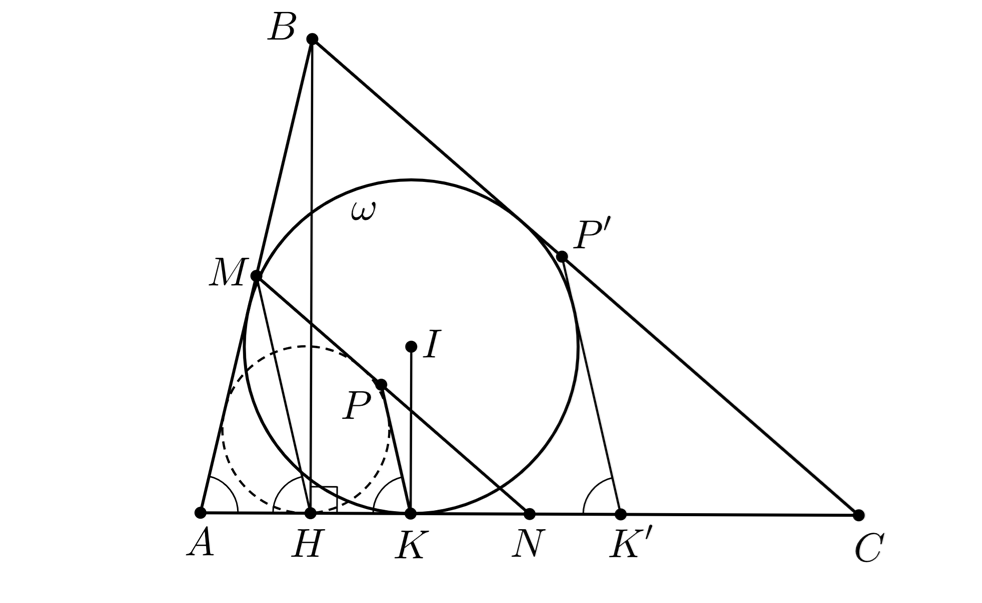
Первое решение. Совершим гомотетию с центром и коэффициентом При этой гомотетии точки и переходят в и соответственно; пусть точки и переходят соответственно в и Тогда достаточно доказать, что четырёхугольник описан. Мы докажем, что он описан около вписанной окружности треугольника Три стороны четырёхугольника уже касаются поэтому достаточно доказать, что её касается

Пусть — центр Тогда поэтому и симметричны относительно Далее заметим, что

Но — медиана в прямоугольном треугольнике поэтому Значит, Значит, и прямые и также симметричны относительно поскольку одна из них касается то и другая тоже. Это и требовалось доказать.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. У решения выше есть несколько вариантов. Например, похожими рассуждениями можно показать, что в четырёхугольнике биссектрисы трёх углов и проходят через одну точку — середину отрезка Отсюда следует, что эта середина — центр искомой вписанной окружности.

_________________________________________________________________________________________________________________________________________________________________________________

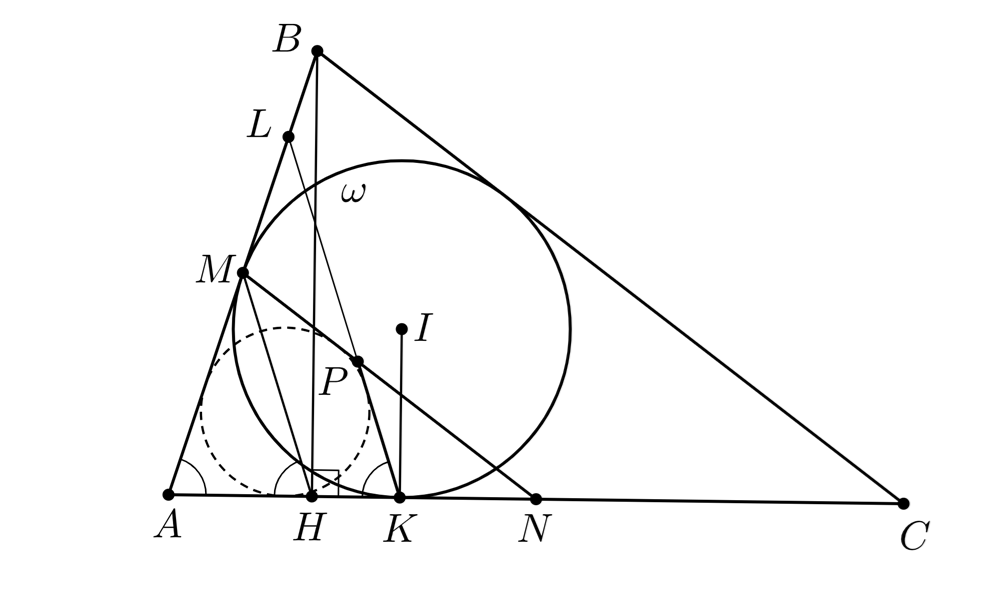
Второе решение. Пусть прямая пересекает прямую в точке Как и в решении выше, получаем, что

откуда

Мы докажем, что окружности, вписанные в треугольники и совпадают (тогда это и будет вписанная окружность четырёхугольника ). Поскольку обе окружности вписаны в угол для этого достаточно показать, что они касаются прямой в одной и той же точке. Как известно, расстояния от до точек касания этих окружностей с равны соответственно

Значит, нам надо доказать, что

или что

Обозначим полупериметр треугольника через и пусть Имеем

С другой стороны,

откуда и следует искомое равенство.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. Во втором абзаце решения по сути доказан следующий известный признак: четырёхугольник описан тогда и только тогда, когда (где и — точки пересечения продолжений боковых сторон, расположенные как на рисунке).