Касание с окружностью и касание окружностей

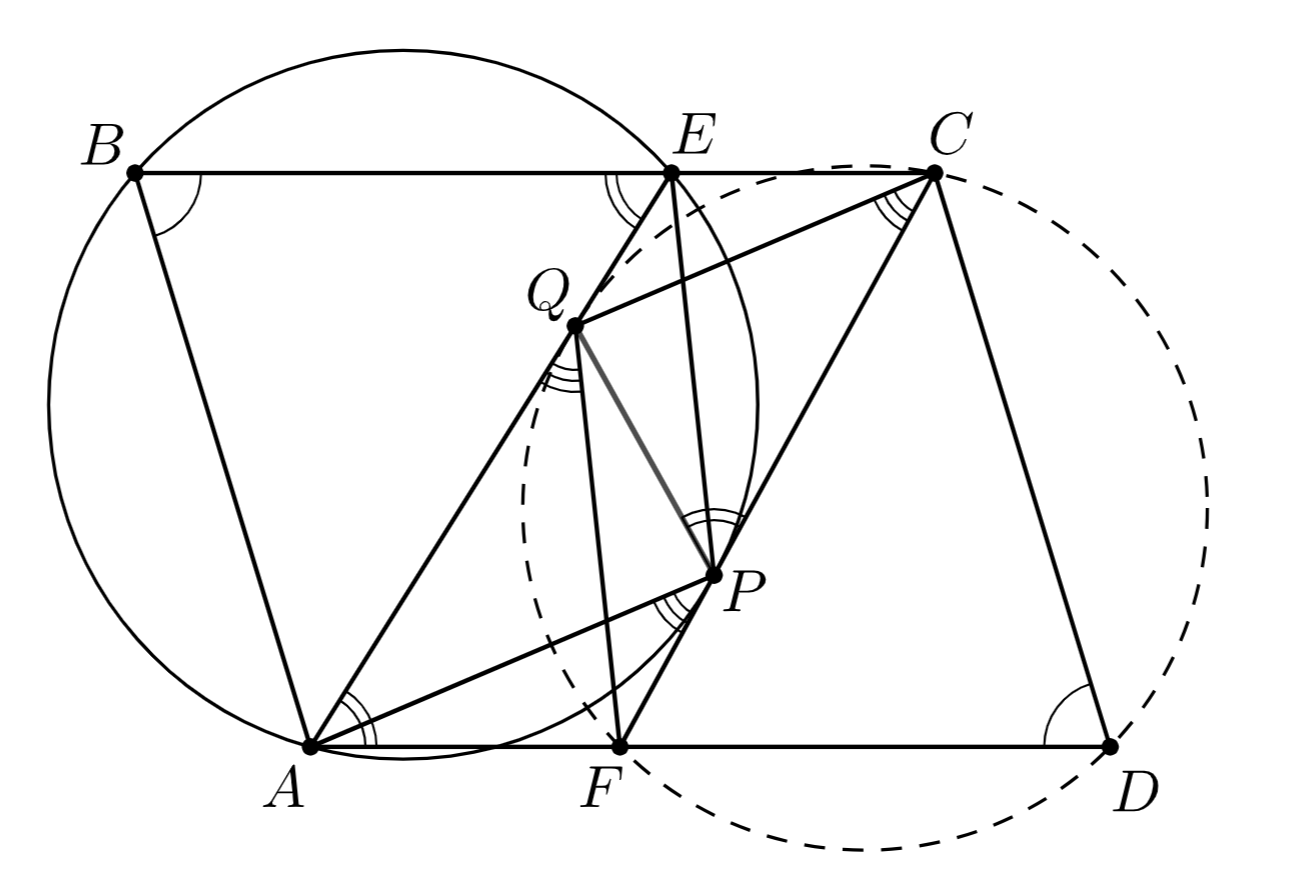
Первое решение. Обозначим точку касания окружности с отрезком через Пусть прямая, проходящая через и параллельная пересекает отрезок в точке (см. первый рисунок). Тогда

(из упомянутых выше касания и параллельности). Значит, четырёхугольник вписанный. Имеем

Следовательно, четырёхугольник вписанный. Тогда

откуда Значит, прямые и ограничивают параллелограмм, откуда Так как

то точка лежит на окружности Раз то окружность касается отрезка в точке что и требовалось.

Второе решение. Обозначим через центр окружности пусть — её радиус и — расстояние от точки до прямой Обозначим через центр окружности пусть — её радиус и — расстояние от точки до прямой Мы докажем более общий факт:

В частности, если то и первое равносильно касанию прямой и окружности второе — касанию прямой и окружности

Если то точки и а также и симметричны относительно центра параллелограмма, и в силу этой центральной симметрии и откуда следует

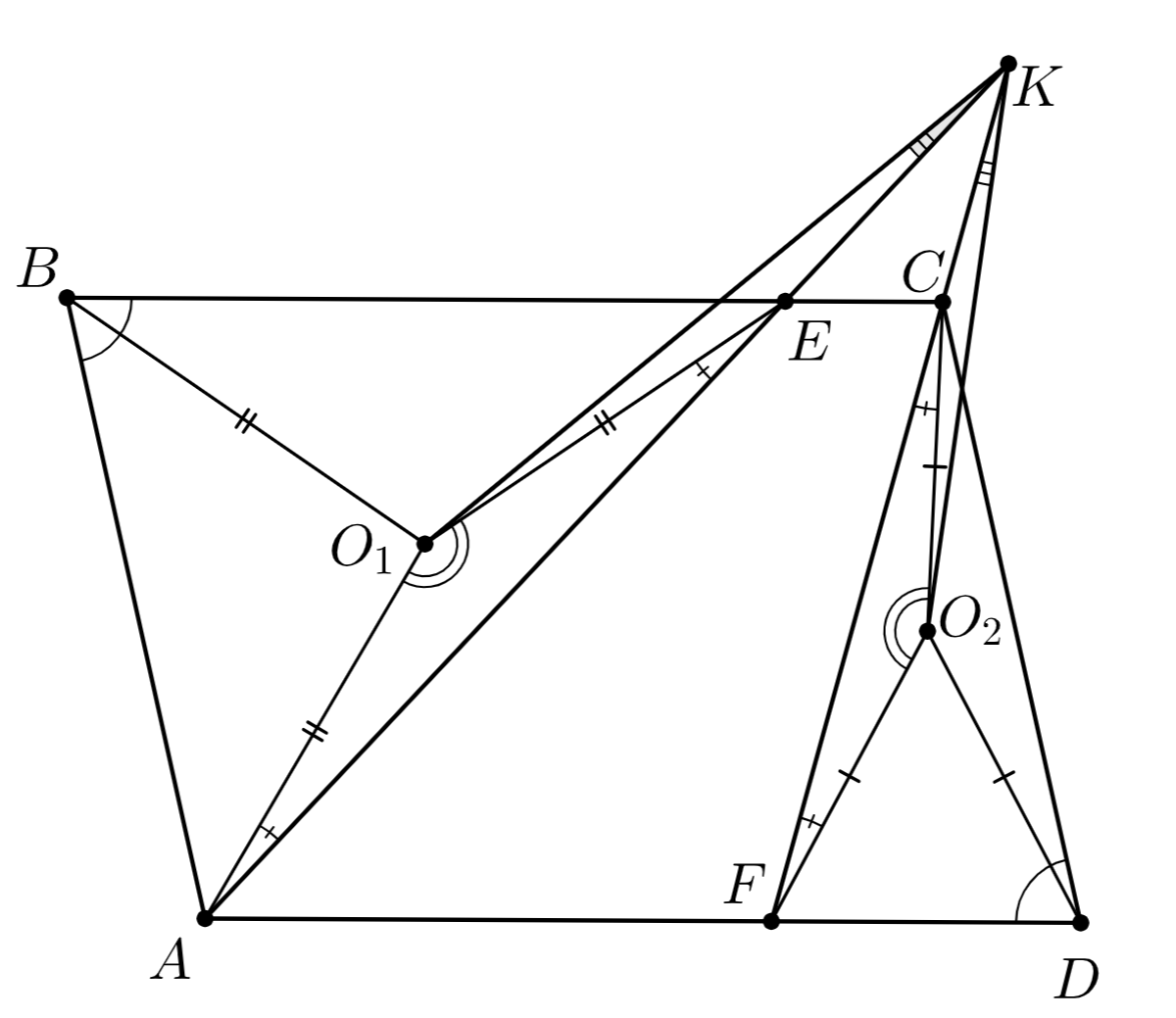
Иначе без ограничения общности будем считать, что луч пересекает луч обозначим их точку пересечения через (см. второй рисунок).

Обозначим через углы при вершинах и параллелограмма Разберём случай в других случаях рассуждение аналогично. Тогда

поэтому равнобедренные треугольники и подобны, откуда и

(последнее равенство следует из теоремы Фалеса). Следовательно, треугольники и подобны по углу и отношению заключающих сторон. Значит,

и Тогда следовательно,

что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. Соотношение () равносильно тому, что угол между окружностью и прямой равен углу между окружностью и прямой

______________________________________________________________________________________________________________________________________________________

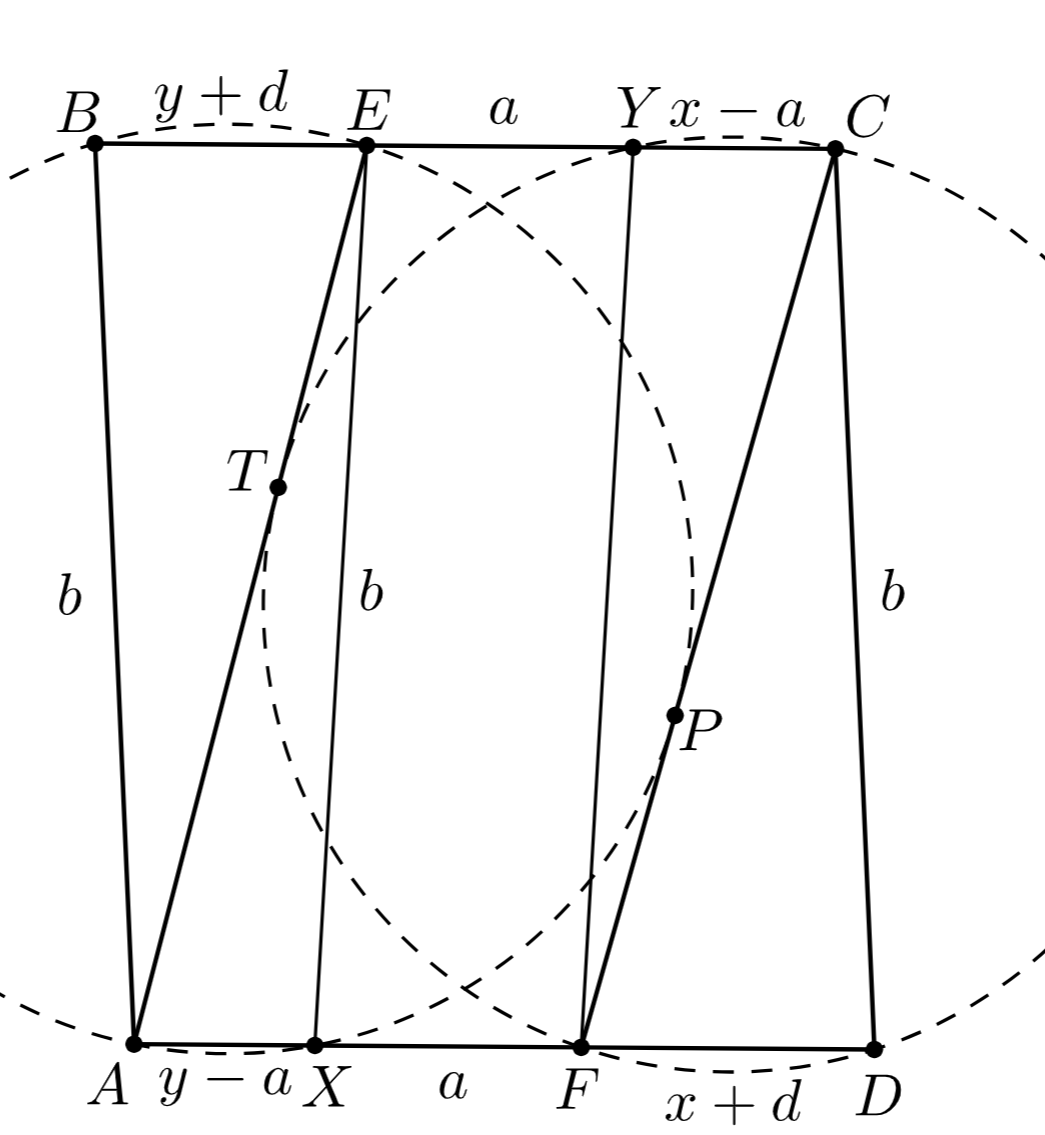
Третье решение. Пусть окружность касается отрезка в точке и вторично пересекает прямую в точке Обозначим вторую точку пересечения окружности с прямой через (см. третий рисунок). Тогда отрезки и симметричны относительно серединного перпендикуляра к а отрезки и — относительно серединного перпендикуляра к поэтому Поскольку окружность касается отрезка то точка лежит на луче Значит, точка лежит на луче причём

Поскольку окружность касается отрезка в точке и Значит,

Мы позднее докажем, что отсюда следует равенство

сначала завершим решение задачи с его помощью: отметим на отрезке точку так, что

и

Если точка отлична от концов отрезка полученные равенства означают, что окружности и касаются прямой в точке Если эти окружности не совпадают, то они обе не совпадают и с окружностью но в таком случае и — радикальные оси этих трех окружностей. Однако, прямые и пересекаются в точке не лежащей на прямой противоречие. Значит, на самом деле окружности и совпадают, а тогда это и есть окружность и она касается в точке Если точки и совпадают, нужно, как обычно, под окружностью понимать окружность, проходящую через и касающуюся в точке

В случае, когда совпадает с одним из концов отрезка возможна лишь ситуация и тогда то есть а также Итого, окружность касается в точке

Остаётся доказать соотношение Положим Из сказанного выше, векторы равны по длине, обозначим её а также равны их проекции на ось, сонаправленную вектору обозначим такую проекцию Положим Тогда и По теореме Птолемея для четырёхугольников и мы получаем, что

и

Отметим, что эти равенства будут выполняться вне зависимости от взаимного расположения точек и и Итого, соотношение имеет вид

После возведения в квадрат и сокращения общих слагаемых, получается симметричное по и равенство:

Следовательно,

а это в точности соотношение что и требовалось.