Касание с окружностью и касание окружностей
Ошибка.
Попробуйте повторить позже
Окружность, вписанная в угол с вершиной касается его сторон в точках
и
— произвольная точка на меньшей из двух дуг
этой окружности. На прямой
взята точка
такая, что прямые
и
параллельны. Пусть
— точка пересечения
окружности
описанной около треугольника
с прямой
отличная от
Докажите, что прямая
касается окружности
Подсказка 1
В задаче есть какие-то углы. Никогда не бывает лишним поотмечать уголочки. Можно заметить вписанность, коллинеарность, подобие. Найдите что-нибудь из этого в этой задаче.
Подсказка 2
Оказывается, что можно понять многое счетом углов. Докажите, что ABMO - вписанный, BKM - равнобедренный. Поймите, как перейти от равнобедренности к касанию.
Подсказка 3
Касательная в вершине равнобедренного треугольника имеет понятное направление. Тогда нужно доказывать, что OM || BK. Поймите это, посчитав углы.
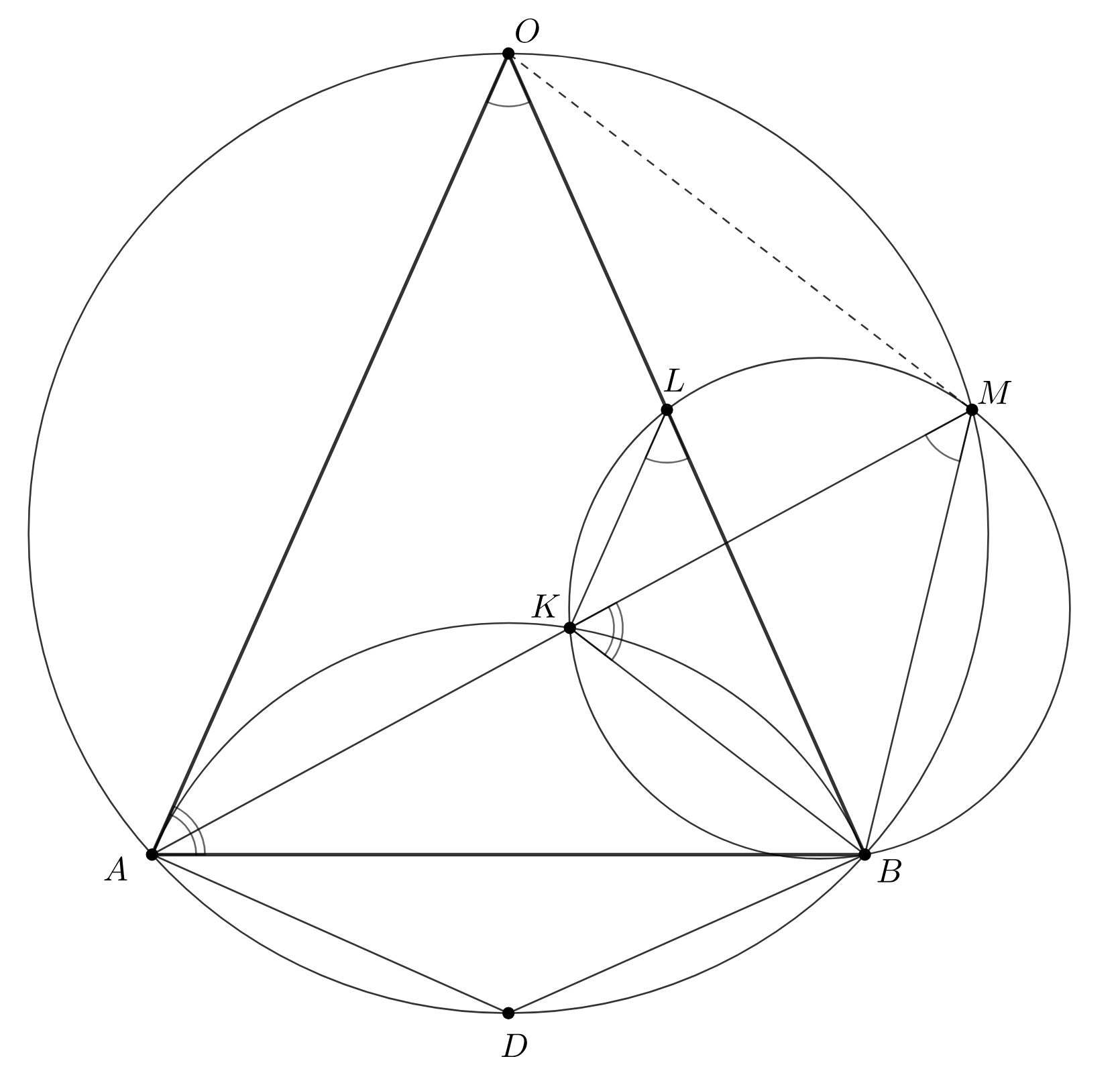
Первое решение. Заметим, что прямые и
антипараллельны в углу, который образован прямыми
и
а значит,
прямые
и
антипараллельны в нем же, то есть четырёхугольник
— вписанный.
Пусть прямая повторно пересекает окружность
в точке
Из вписанности четырёхугольника
следует, что прямые
и
антипараллельны в углу, образованном прямыми
и
но в этом же углу прямые
и
также
антипараллельны, следовательно, прямая
параллельна прямой
Теперь рассмотрим угол В нём прямые
и
антипараллельны, а значит, прямые
и
тоже антипараллельны,
что эквивалентно касанию прямой
и окружности
![]()
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Покажем, что лежит на окружности
Действительно,
откуда имеем
требуемое.
Докажем, что Пусть
— точка, диаметрально противоположная точке
в окружности
Тогда
Тогда, поскольку
— центр описанной окружности
следовательно,
Кроме этого, в силу вписанности четырехугольника
Таким образом, треугольник
подобен
треугольнику
следовательно, является равнобедренным.
Наконец, — биссектриса внешнего угла
поскольку
— центр дуги
окружности
следовательно,
то есть, поскольку
— середина дуги
окружности
прямая
касается
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




