Степень точки и радикальные оси
Ошибка.
Попробуйте повторить позже
Пусть — параллелограмм, отличный от прямоугольника, а точка
выбрана внутри него так, что описанные окружности
треугольников
и
имеют общую хорду, перпендикулярную
Докажите, что радиусы данных окружностей
равны.
Источники:
Подсказка 1
Часто в геометрии полезно избавиться от ненужных объектов на картинке. В данном случае это общая хорда окружностей. Как можно переформулировать то что она перпендикулярна AD?
Подсказка 2
Это равносильно тому, что линия центров окружностей параллельна AD!
Подсказка 3
Теперь посмотрите на картинку повнимательнее: между двумя окружностями, которые должны быть равны, есть много общего...
Подсказка 4
Центры обеих окружностей лежат на линии центров, параллельной AD, а также центр первой лежит на...
Подсказка 5
Серединном перпендикуляре к AB! А центр второй - на серединном перпендикуляре к CD. Теперь просто нужно понять, что картинка (AB и центр первой окружности) равна картине (CD и центр второй окружности).
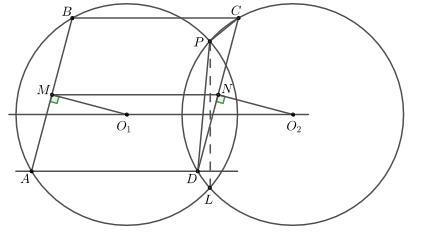
Первое решение.
Заметим, что линия центров перпендикулярна общей хорде данных окружностей, а значит параллельна прямым
и
Пусть
- середина отрезка
- середина отрезка
Тогда
и, поскольку
прямые
и
параллельны. Далее,
и при этом
поэтому
Заключаем, что четырёхугольник
—
параллелограмм по определению, следовательно
Кроме того, поскольку отрезки
и
равны, то по двум катетам
будут равны прямоугольные треугольники
и
следовательно, равны их гипотенузы
и
являющиеся также
радиусами наших окружностей, что и требовалось доказать
Первое решение.
Предположим противное, радиусы окружностей и
описанных около треугольников
и
соответственно,
различны.
При параллельном переносе на отрезок
перейдет в отрезок
окружность
перейдёт в окружность
а прямая
перейдёт в себя. Причём
не может совпадать с
поскольку их радиусы различны. Поэтому
линия центров
совпадающая с прямой
перпендикулярна общей хорде
Таким образом, прямая
параллельна общей хорде окружностей
и
и, следовательно, перпендикулярна прямой
Но тогда параллелограмм
является прямоугольников, что противоречит условию задачи. Следовательно, радиусы окружностей
и
равны.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




