Четырёхугольники в окружности, счёт отрезков и углов, теорема Птолемея
Ошибка.
Попробуйте повторить позже
Докажите, что в неравнобедренном треугольнике расстояние от точки Фейербаха до середины одной из сторон равно сумме расстояний от точки Фейербаха до середин двух других.
Подсказка 1
Пусть ABC — исходный треугольник, M_a, M_b, M_c — середины стороны BC, AC, AB соответственно, ω — вписанная окружность, F — точка Фейербаха.. Как мы можем воспользоваться касанием ω и (M_aM_bM_c), чтобы получить условие на отрезки вида M_aF?
Подсказка 2
Можем воспользоваться теоремой Кэзи для окружностей M_c, F, ω, M_b. Какое условие на отрезки M_cF и M_bF мы получим?
Подсказка 3
K_a, K_b, K_c — точки касания ω с соответствующими сторонами. Мы имеем, что FM_c/FM_b = M_cK_c/M_bK_b и аналогичные. Как это позволяет переписать исходное условие в терминах отрезков вида M_cK_c?
Подсказка 4
Вместо того, чтобы доказывать (FM_c + FM_b) / FM_a = 1, будем доказывать, что (M_cK_c + M_bK_b) / M_aK_a = 1. Как данные отрезки выражаются через стороны треугольника?
Подсказка 5
Без ограничений общности будем считать, что AB ≥BC ≥ CA. Тогда M_cK_c = (BC - CA) / 2; M_bK_b = (AB − BC) / 2; MaKa = (AB - AC) / 2. Завершите доказательство.
Пусть — исходный треугольник,
— середины стороны
соответственно,
— вписанная окружность,
— точки касания
с соответствующими сторонами,
— точка Фейербаха.
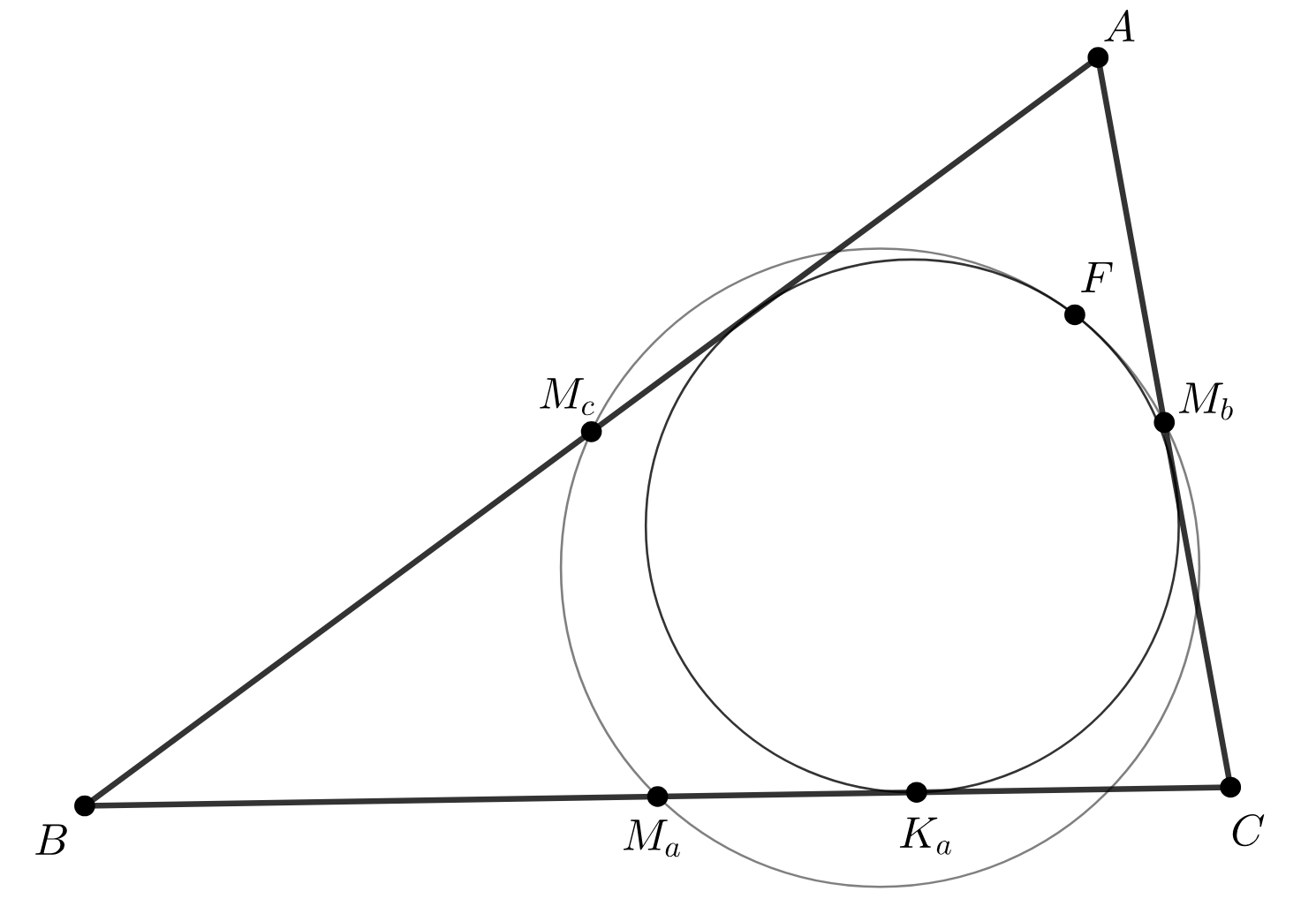
По теореме Кэзи для имеем
следовательно,
Аналогично,
Без ограничений общности будем считать, что Тогда
следовательно,
что завершает доказательство.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




