Треугольник с углом 60 градусов
Ошибка.
Попробуйте повторить позже
Диагонали выпуклого четырёхугольника 
пересекаются в точке 
и при этом треугольники 
и 
—
правильные. Точка 
симметрична точке 
относительно середины стороны 
Докажите, что 
— правильный
треугольник.
Источники:
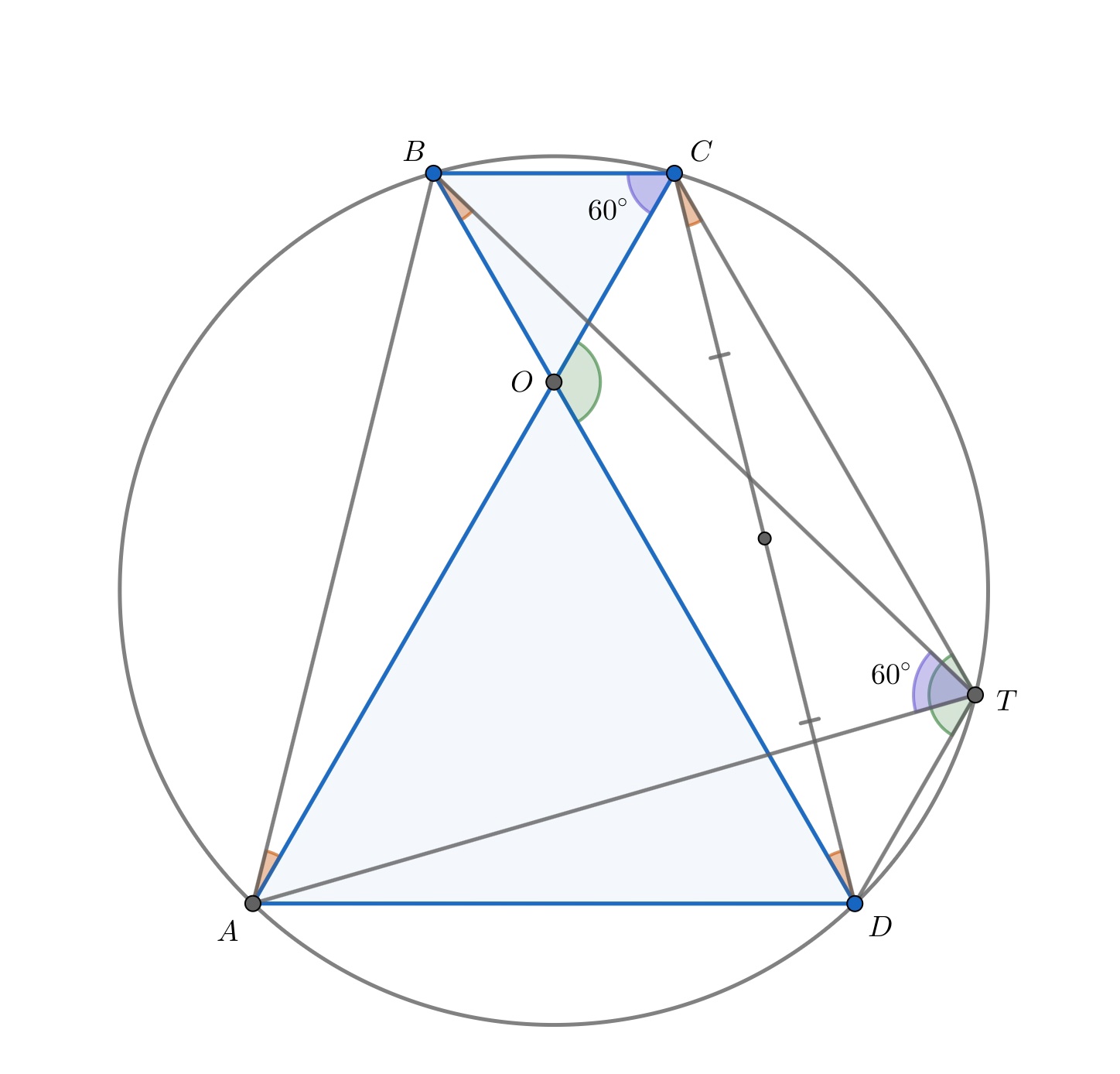
Несложно показать, что 
— равнобедренная трапеция, поэтому вокруг неё можно описать окружность (назовём
её 
. Диагонали четырёхугольника 
точкой пересечения делятся пополам, поэтому он параллелограмм, и при
этом
Поскольку 
, в четырёхугольнике 
сумма противоположных углов равна 
, и вокруг него также можно описать
окружность. Следовательно, все 5 точек 
лежат на окружности 
. Углы 
и 
вписаны в 
и опираются на одну
дугу, поэтому они равны, и 
. Далее отметим, что
Отсюда следует, что
Итак, доказано, что в треугольнике 
два угла равны 
, поэтому он равносторонний.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
