Удвоение
Ошибка.
Попробуйте повторить позже
Внутри прямоугольного треугольника с прямым углом при вершине
отмечена точка
причём
Известно также,
что
— высота треугольника
точка
— середина отрезка
Найдите
Подсказка 1:
Начнём подсказки с важной леммы. Пусть в прямоугольнике есть точка O, и известны расстояния от неё до трёх вершин прямоугольника. Тогда можно вычислить расстояние до четвёртой. Это делается с помощью нескольких теорем Пифагора, обоснуйте этот факт.
Подсказка 2:
Наверное, вы задались вопросом, зачем нужна эта лемма и как её применить в задаче, ведь здесь даже нет прямоугольника? Его нет, а вот прямоугольный треугольник — есть. Если удвоить медиану, проведённую к гипотенузе, то получится прямоугольник.
Подсказка 3:
Будем искать длину CO. Расстояния от O до B и A известны, осталось вычислить расстояние от O до F.
Подсказка 4:
Обратите внимание, EM — средняя линия в треугольнике OCF. Значит, всё свелось к нахождению длины EM.
Подсказка 5:
Обратите внимание на треугольник DEM. Что про него можно сказать?
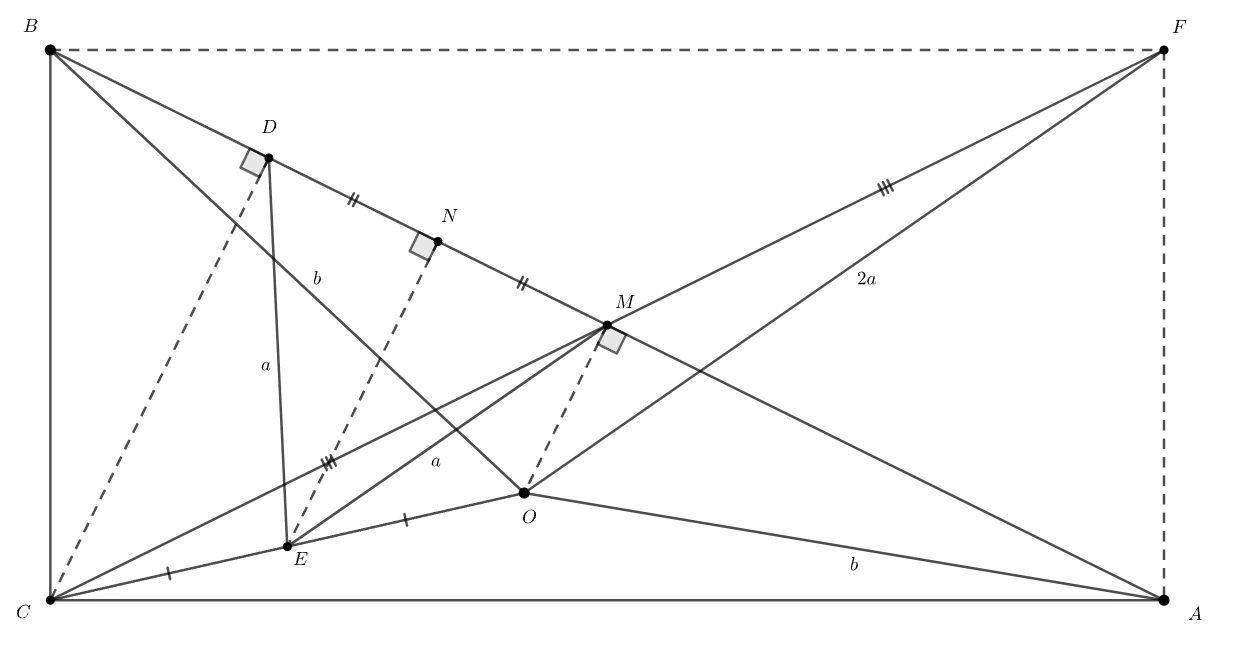
Пусть и
— проекции точек соответственно
и
на гипотенузу
Заметим, что
— середина
Поскольку
и
— середина
то
— средняя линия трапеции
поэтому
— середина отрезка
Высота
в
треугольнике
является его медианой, поэтому треугольник
— равнобедренный. Следовательно,
На продолжении отрезка за точку
отложим отрезок
равный
Тогда
— прямоугольник,
— средняя
линия треугольника
Таким образом, нам известны расстояния от точки до трёх вершин прямоугольника
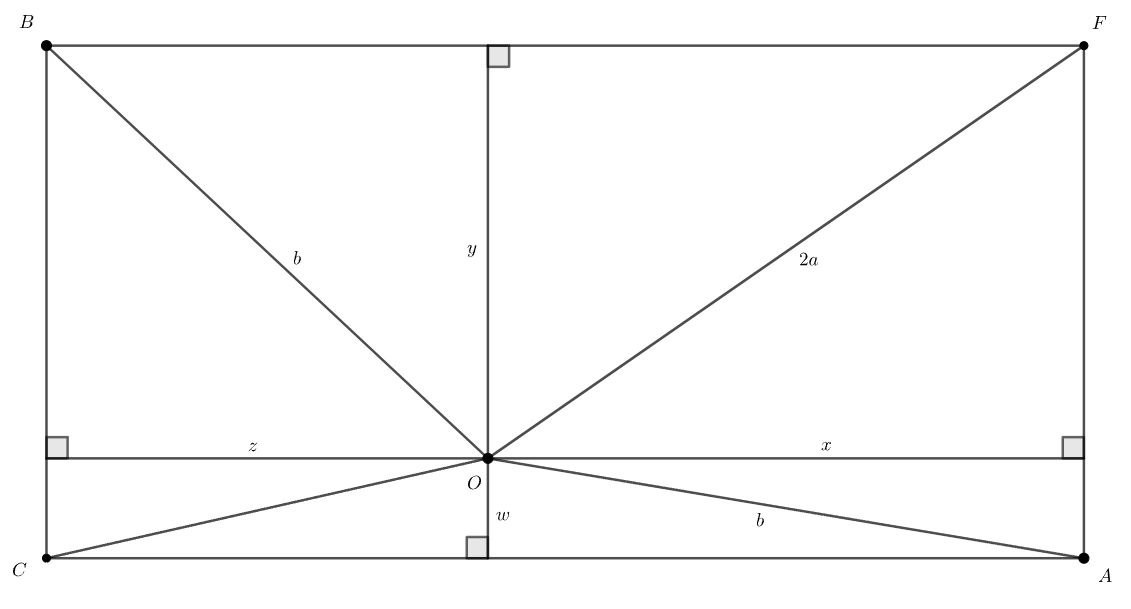
Опустим из точки перпендикуляры на стороны
и
— равные
и
соответственно.
Тогда по теореме Пифагора:
Откуда получаем
Тогда,
Следовательно,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




