Удвоение
Ошибка.
Попробуйте повторить позже
Разрежьте данный параллелограмм на две части, из которых можно составить треугольник. Не забудьте объяснить, как именно составить треугольник и почему образуется именно он.
Подсказка 1
Итак, нам нужны две фигуры, из которых можно составить треугольник. Получается, что эти фигуры нам придётся "склеивать" какой-то стороной, то есть какие-то две стороны у них будут равны между собой. На какое построение намекают эти размышления?
Подсказка 2
Имеет смысл отметить середину у одной из сторон параллелограмма! Осталось лишь придумать, как же провести нужный разрез через неё ;)
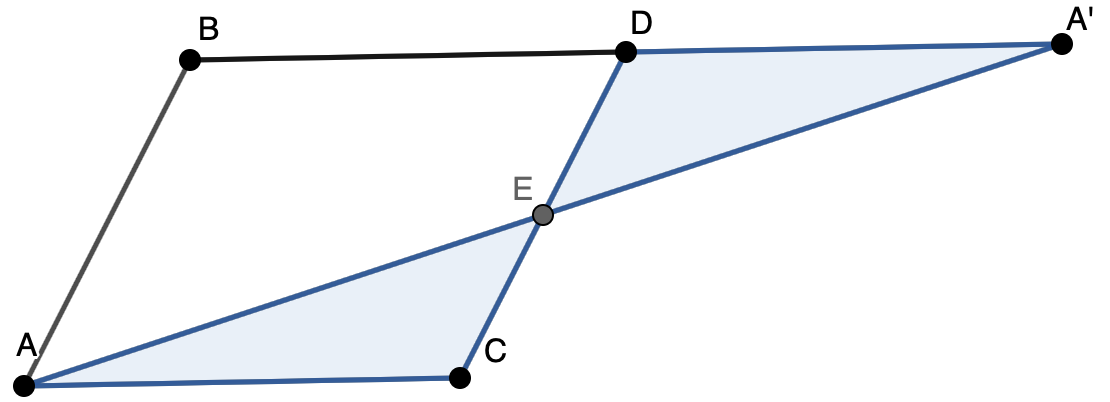
Из параллелограмма получится треугольник
.
Почему это работает? Давайте посмотрим на построение. Точка — середина стороны
. Удвоим
за точку
, получим точку
. Треугольники
и
равны по двум сторонам и углу между ними, так как
по построению,
, потому
что
— середина отрезка
,
как вертикальные. Теперь поймем, почему точки
,
,
лежат на
одной прямой. Для этого достаточно показать, что
. Но это верно, ведь мы поняли, что
треугольники
и
равны, то есть углы
и
равны как соответственные, а так же нам дано, что
—
параллелограмм, значит,
как односторонние при параллельных прямых
и
и секущей
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




