Удвоение
Ошибка.
Попробуйте повторить позже
Из середины стороны параллелограмма противоположная его сторона видна под прямым углом, то есть образует прямой угол с концами этой стороны. Найдите отношение сторон параллелограмма.
Подсказка 1
Пусть E — середина стороны AC параллелограмма ABCD. Пока что BE — просто отрезок внутри четырёхугольника. А что хочется с ним сделать?)
Подсказка 2
Давайте продлим BE за точку E до пересечения с прямой CD в новой точке B'! Что можно сказать про треугольники ABE и CB'E? Не забываем, что в параллелограмме противоположные стороны параллельны, а значит, можно отметить равные углы! (например, накрест лежащие)
Подсказка 3
Отлично, треугольники ABE и CB'E равны по двух углам и стороне между ними (AE = EC). Что тогда можно сказать про связь BE и EB'?
Подсказка 4
Именно, BE = EB'! А давайте теперь вспомним условие ;)
Подсказка 5
Итак, BE = EB', а угол BED — прямой. Что тогда можно сказать про треугольник BB'D?
Подсказка 6
Кем является DE для треугольника BB'D? Что это говорит о треугольнике BB'D?
Подсказка 7
Отлично, треугольника BB'D равнобедренный! Осталось лишь отметить равные отрезки, которые появились из построения и условия, и понять, во сколько раз BD больше, чем DC :)
Пусть — вершины исходного параллелограмма,
— середина стороны
причем
Продлим прямую до пересечения с прямой
в точке
Треугольники
и
подобны в силу параллельности
прямых
и
и равны, поскольку равны их соответствующие стороны
и
а значит,
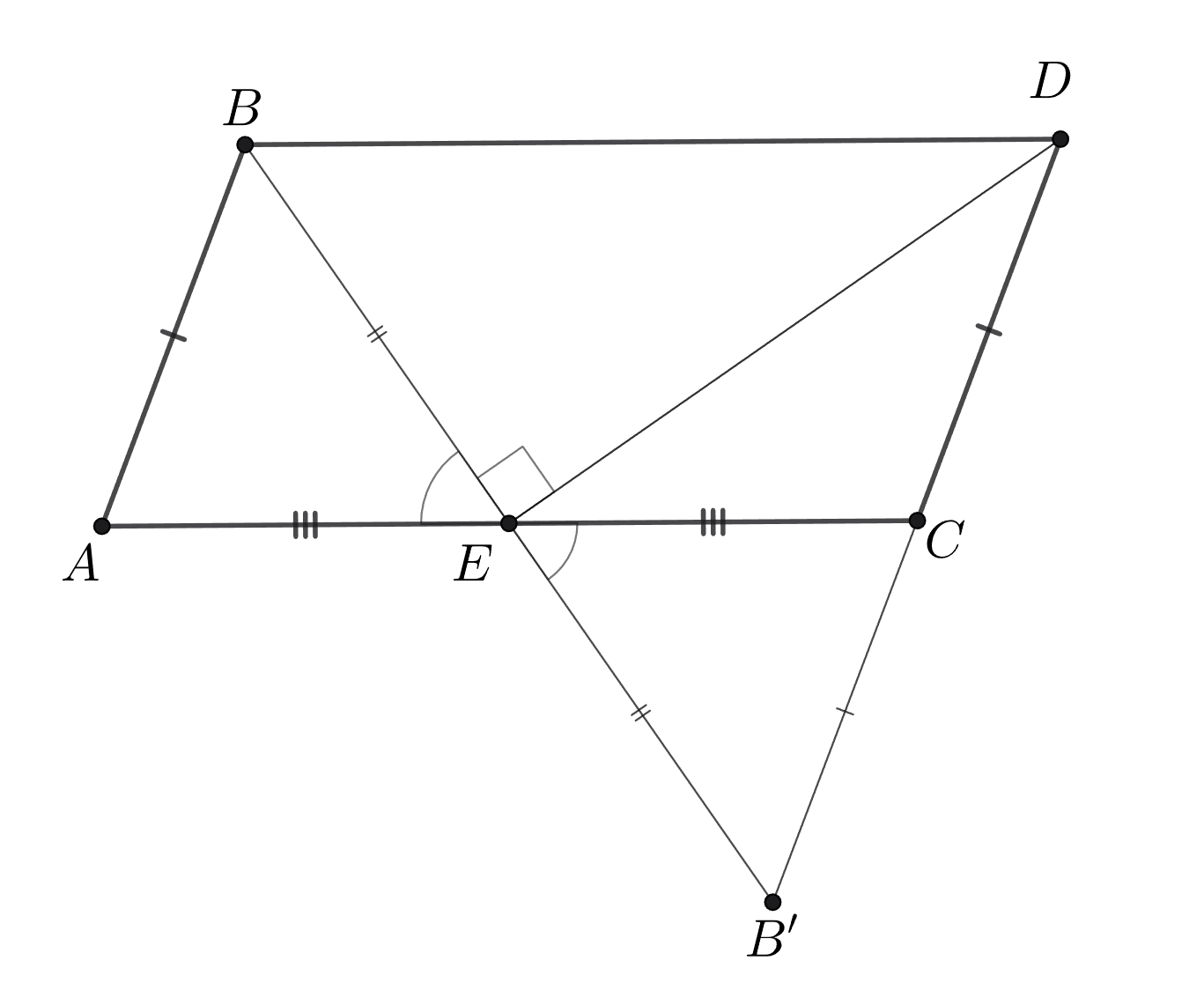
Осталось заметить, что поскольку
— медиана, проведенная из вершины, соответствующей прямому углу. Таким
образом,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




