Удвоение
Ошибка.
Попробуйте повторить позже
В треугольнике точка
— середина стороны
. На стороне
взяли точку
так, что угол
прямой. Оказалось, что
. Найдите
, если
.
Подсказка 1
Как воспользоваться тем, что какой-то отрезок равен AB? Быть может, мы сможем построить ещё один отрезок, равный AB, и записать цепочку равенств?
Подсказка 2
Очень часто в подобных задачах помогает удвоить медиану, так как после этого появляется сторона, равная AB!
Подсказка 3
Итак, удвоим медиану BM до BD. Из теоретического материала мы знаем, что AB = CD (докажите самостоятельно!) А что можно интересного сказать про треугольник BKD? Как воспользоваться условием на прямой угол?
Подсказка 4
Чем является KM в треугольнике BKD?
Подсказка 5
KM и медиана, и высота, так что BKD равнобедренный! Интересно, у нас уже немало отрезков, равных BK ;) Запишем цепочку равенств!
Подсказка 6
CD = AB = BK = KD. О чем это говорит для треугольника KCD? Быть может, мы знаем его углы?
Подсказка 7
Треугольник KCD равнобедренный, а угол MCD равен углу BAM. Чему тогда равен угол KCD?
Подсказка 8
Угол KCD равен 70°! Тогда, так как KCD равнобедренный, мы можем посчитать все остальные его углы ;)
Подсказка 9
Получается, что угол DKC тоже равен 70°! Отлично, мы уже очень близки к нужному углу BKM! Осталось лишь понять, как именно его величина связана с величиной угла BKD и DKC ;)
Пусть — точка, симметричная точке
относительно
Отрезок
является высотой, а так же медианой треугольника
следовательно,
Четырехугольник
является параллелограммом, т.е.
и
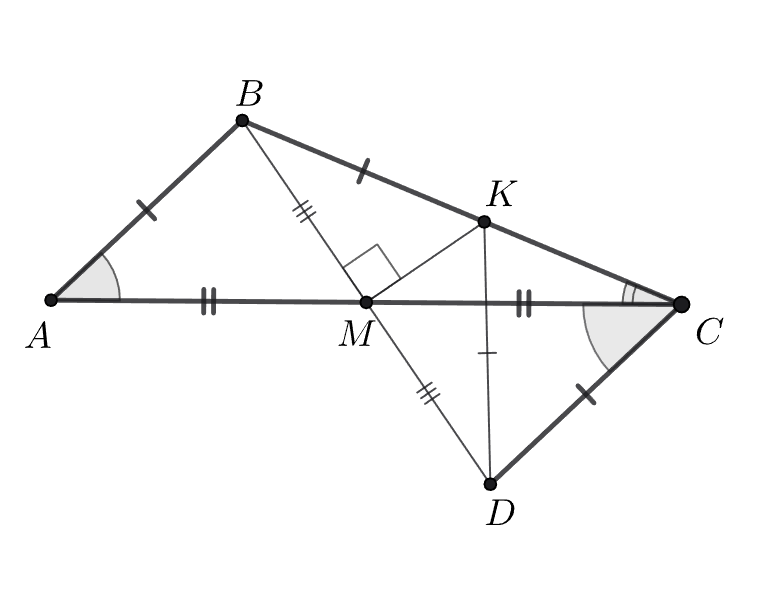
Наконец, а значит,
следовательно,
т.е. поскольку
является биссектрисой угла
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




