Спрямление

Давайте отметим на такую точку что Если докажем равенство то задача решена. Видно, что треугольник — равнобедренный с углами при основании по Также Но тогда

То есть треугольник равнобедренный с углами по при основании.

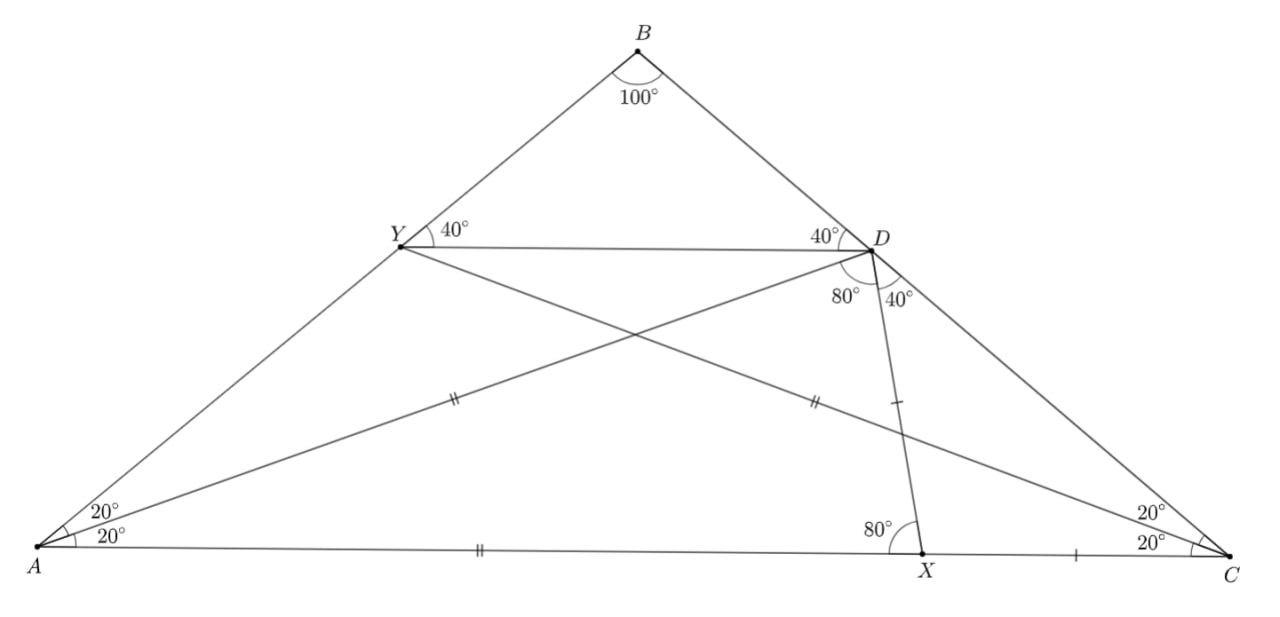
Давайте проведём прямую параллельно Это сделано для того, чтобы получить равнобедренный треугольник с углами по при основании. Заметим, что треугольники и подобны, при этом у одного боковая сторона равна а у другого — То есть, если мы докажем, что коэффициент подобия равен то дело в шляпе. Для этого достаточно доказать равенство оснований и Давайте проведём и заметим, что это биссектриса в треугольнике (чтобы это понять, достаточно сделать симметрию относительно серединного перпендикуляра Значит, Также Теперь из суммы углов треугольника ясно, что треугольник равнобедренный, что даёт требуемое.