Центральная симметрия
Ошибка.
Попробуйте повторить позже
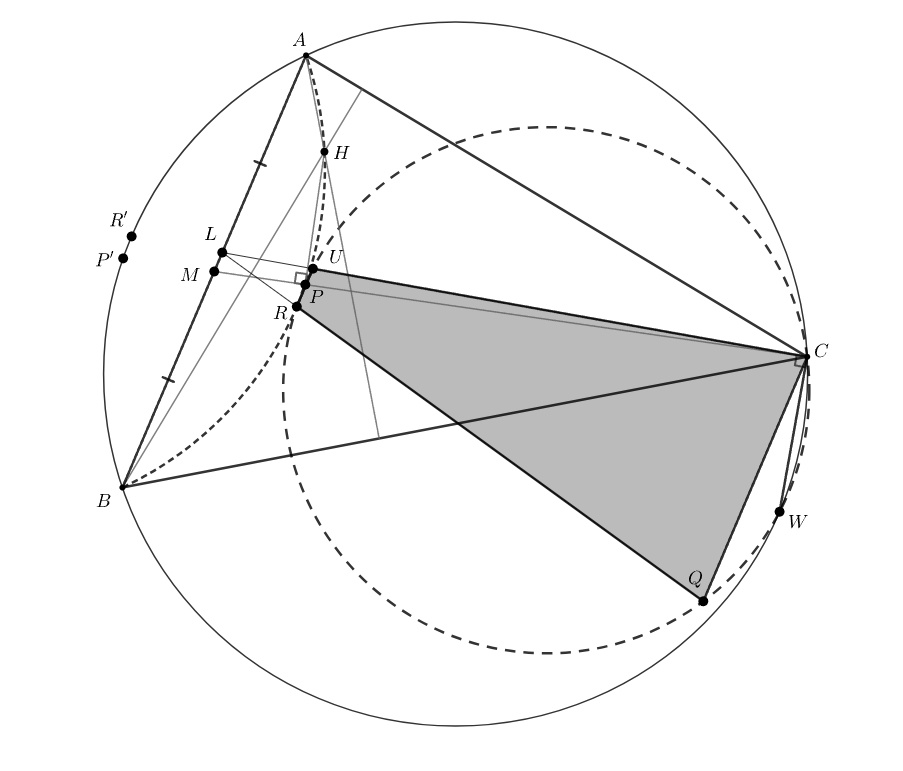
Дан треугольник Пусть
— его биссектриса,
— середина дуги
а
— проекиия ортоцентра на медиану, проведённую
из вершины
Окружность
пересекает прямую, проходящую через
и параллельную
в точке
Докажите, что
Источники:
Подсказка 1
Внимательно посмотрите на картинку и отметьте все (на ваш взгляд) необходимые точки пересечения. Как можно было бы доказать нужное равенство? Быть может, можно найти какую-то полезную фигуру? Интуитивно понятно, что нам нужны новые объекты - давайте их проводить!
Подсказка 2
Проведите окружности CPW и AHB и изучите их точки пересечения. Что можно сказать про связь точки P с ними?
Подсказка 3
Точка P — пересечение медианы с дугой окружности AHB.
Подсказка 4
Докажите, что середина дуги AHB лежит на окружности CPW. А что можно сказать про отрезок, соединяющий точки пересечения указанных окружностей?
Подсказка 5
Докажите параллельность отрезка, соединяющего точки пересечения окружностей (AHB) и (CPW), и отрезка CQ.
Первое решение. Известно, что точка — пересечение медианы с дугой
Пусть
— середина этой дуги, а
—
середина
Точки
и
симметричные
и
относительно
лежат на описанной окружности
поэтому
откуда заключаем, что принадлежит окружности
Далее, так как луч
пересекает окружность
в точке
диаметрально противоположной точке
следовательно,
Отсюда
— средняя линия треугольника
то есть
— середина отрезка
Во вписанной трапеции
общий серединный перпендикуляр к
и
проходит через
что и даёт требуемое.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Пусть — точка на прямой
такая, что
Докажем, что точки
лежат на одной
окружности.
Рассмотрим композицию инверсии с центром и симметрии относительно
которая взаимно обменяет вершины
и
Эта же
композиция меняет местами прямую
и описанную окружность треугольника, поэтому
переходит в середину
дуги
а
—
в основание
внешней биссектрисы угла
точка Шалтая
переходит в точку пересечения касательных к окружности
проведённых в
и
Прямая при этом перейдёт в касательную к окружности
в точке
а окружность с центром
проходящая через
перейдёт в серединный перпендикуляр к
(поскольку образы точек
и
инверсны относительно этой окружности). Следовательно,
переходит в точку пересечения касательных в
и
Эта точка, образ точки и точка
лежат на одной прямой — поляре точки
относительно окружности
что завершает
доказательство.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




