Центральная симметрия
Ошибка.
Попробуйте повторить позже
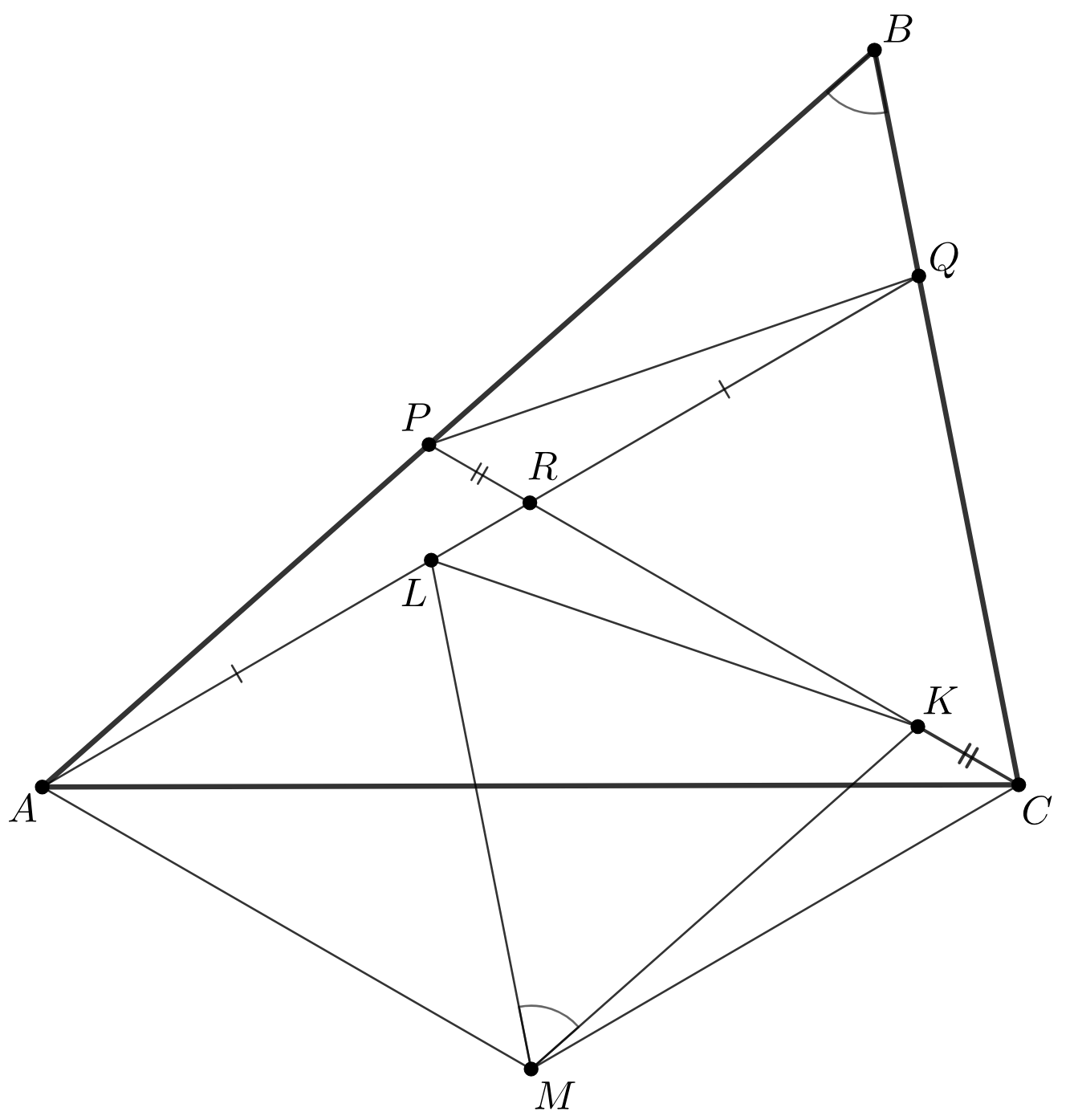
На сторонах 
и 
треугольника 
выбраны точки 
и 
соответственно. Отрезки 
и 
пересекаются в точке 
Оказалось, что 
Докажите, что из отрезков 
и 
можно составить треугольник, один из углов которого
равен углу 
Источники:
Отметим точки 
и 
на отрезках 
и 
соответственно таким образом, чтобы 
а 
Рассмотрим точку 
симметричную 
относительно середины отрезка 
Нетрудно показать, что четырёхугольники 
и 
—
параллелограммы, поэтому треугольник 
— искомый. В самом деле, 
(так как прямые
и 
ограничивают параллелограмм), 
и, аналогично, 
откуда
и 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
