Осевая симметрия
Ошибка.
Попробуйте повторить позже
В пространстве расположены отрезки
и
с общей серединой
Оказалось, что сфера
описанная около тетраэдра
касается плоскости
в точке
Точка
— центр окружности, описанной около треугольника
Докажите, что
Источники:
Подсказка 1
Каким способом можно доказывать равенство двух отрезков? Может, стоит найти третий отрезок, который будет равен одному из иcходных?
Подсказка 2
Действительно, у нас уже есть пары равных отрезков AM и A'M, BM и B'M, CM и C'M. В частности, это говорит о том, что треугольники ABC и A'B'C' симметричны относительно точки M. Как построить отрезок, равный OM, связь которого со сферой была бы более естественна, чем та же у последнего?
Подсказка 3
Если O' — центр описанной окружности треугольника A'B'C', то OM=M'O. Как эти точки связаны с D?
Подсказка 4
На самом деле, касание сферы и плоскости влечет равенство угла ODO' прямому. Осталось понять, чем является точка M в треугольнике ODO'.
Обозначим через центр окружности, описанной около треугольника
через
— центр сферы
(см. рис.). При центральной
симметрии относительно точки
треугольник
переходит в треугольник
Следовательно, точки
и
симметричны
относительно точки
то есть
— середина отрезка
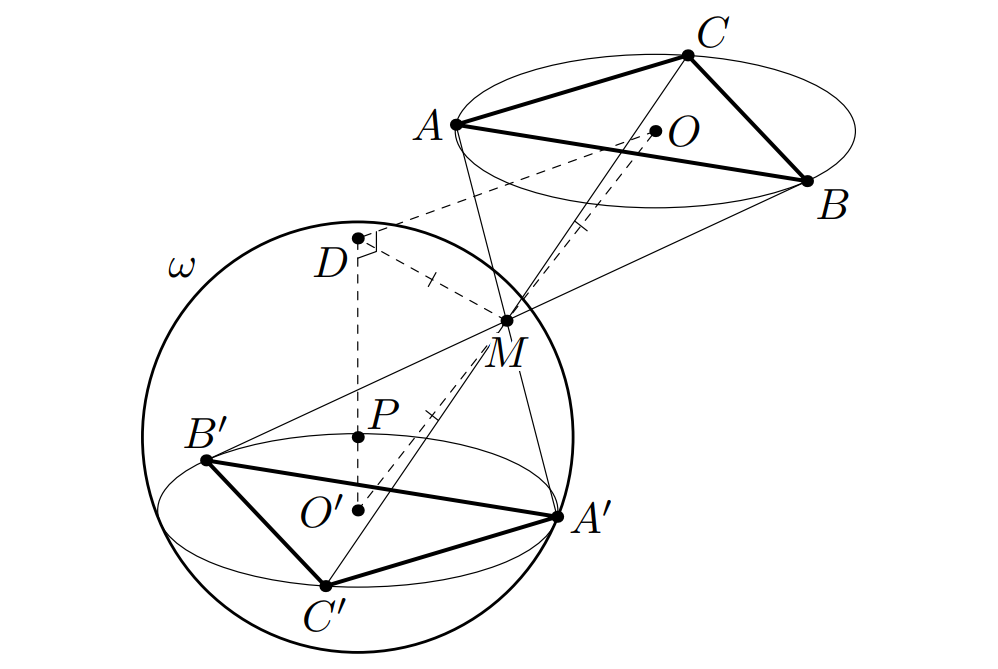
Также мы получаем, что плоскости и
параллельны. Тогда на прямой, проходящей через точку
перпендикулярно этим
плоскостям, лежат точки
и
поэтому
Таким образом,
— медиана в прямоугольном треугольнике
значит,
что и требовалось.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




