Поворот

Первое решение

Построим серединный перпендикуляр к отрезку обозначим за и точки его пересечения со сторонами и соответственно.

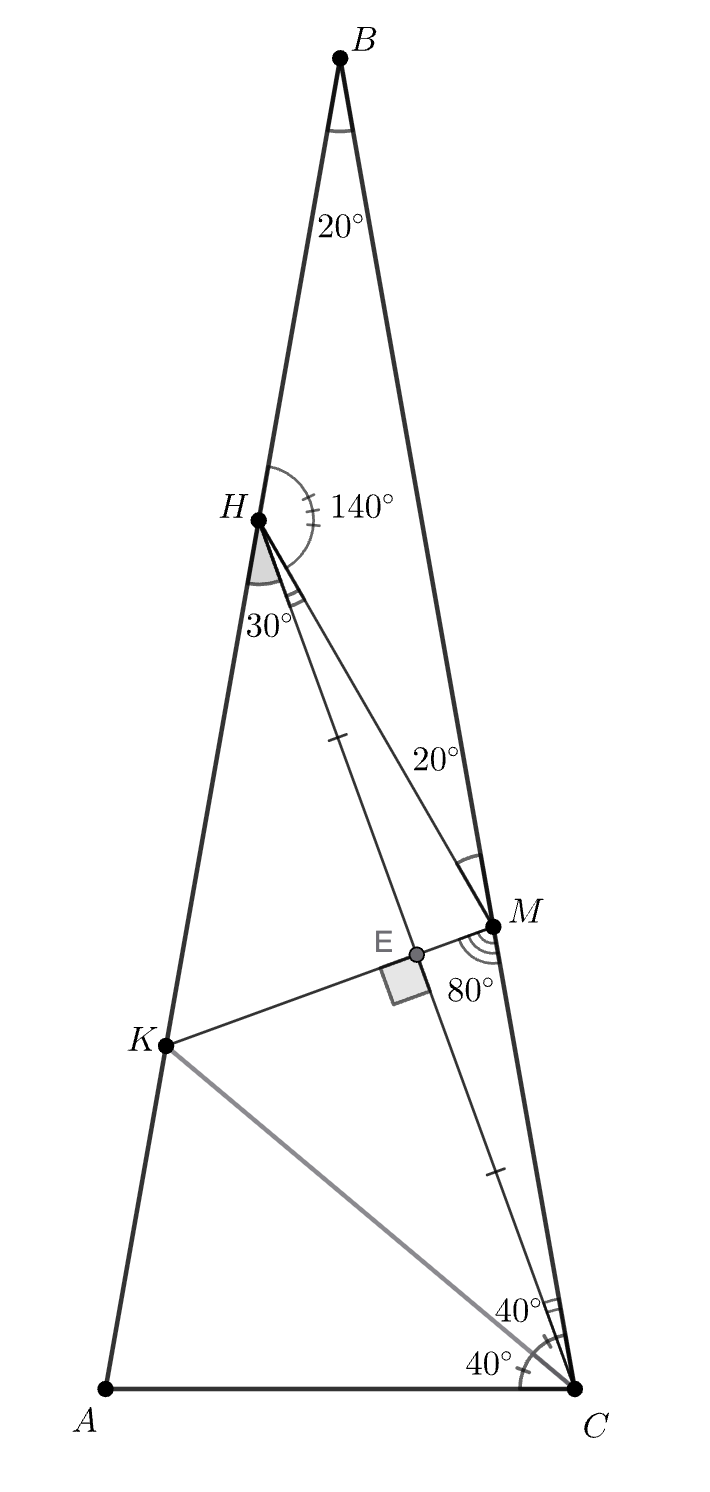
Треугольник — равнобедренный с углами при основании поэтому отрезки и равны как его боковые стороны.

В треугольнике

Кроме того,

Следовательно, треугольник — равнобедренный с боковыми сторонами и Получаем, что Теперь посмотрим на равнобедренный треугольник с Следовательно,

Заметим, что

Тогда — биссектриса угла

Треугольники и равны по общей стороне и по 2 углам Тогда

Получаем, что

______________________________________________________________________________________________________________________________________________________

Второе решение

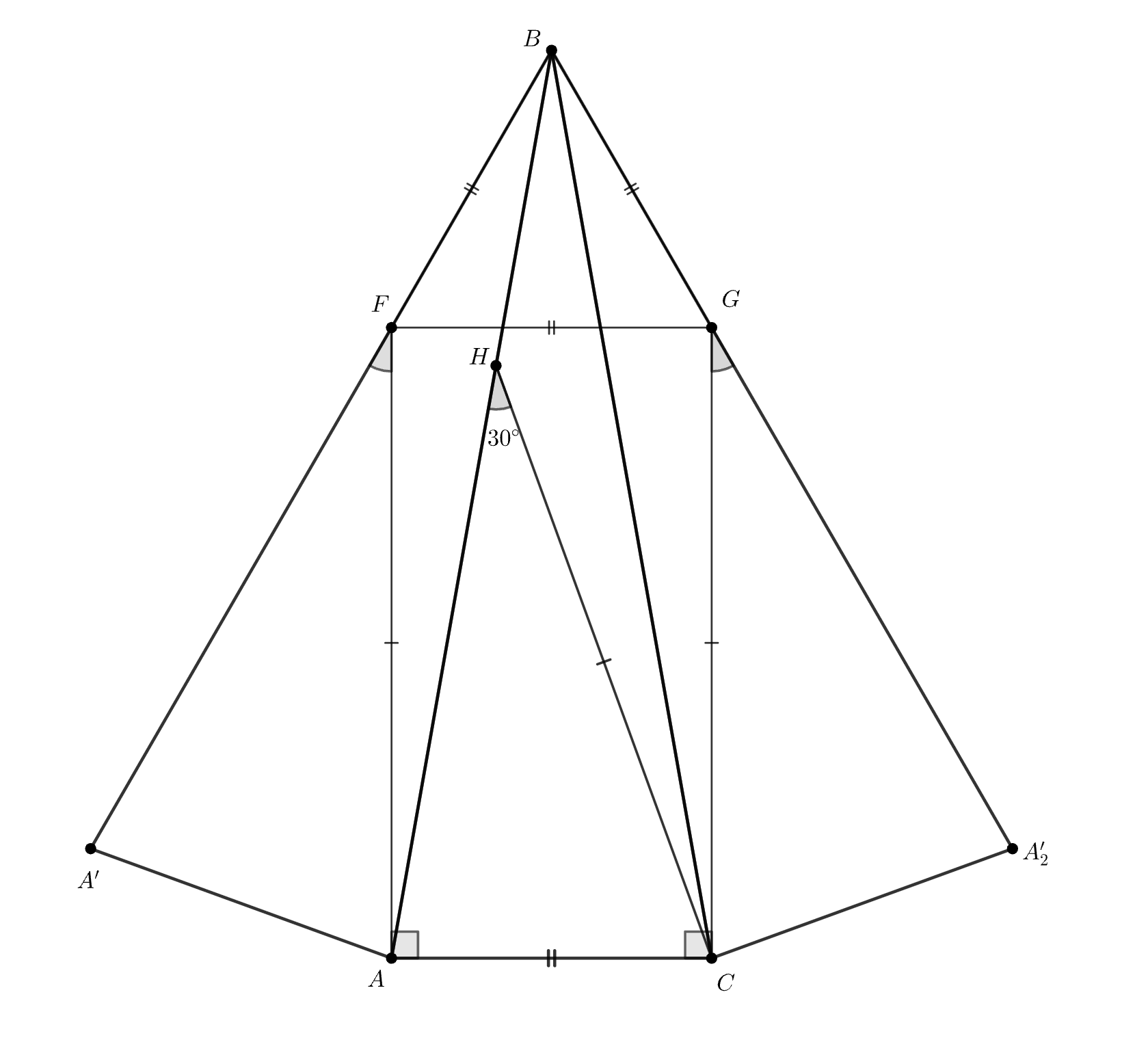
Повернём треугольник вокруг точки по часовой стрелке на чтобы сторона совместилась со стороной Образ точки при этом повороте обозначим за Затем зеркально отразим треугольник относительно стороны образ точки при этом отражении обозначим за

Тогда четырехугольник является прямоугольником и

В треугольнике по построению а также

Следовательно, треугольник — равнобедренный с углом при вершине, а значит, он является равносторонним. Тогда

______________________________________________________________________________________________________________________________________________________

Третье решение

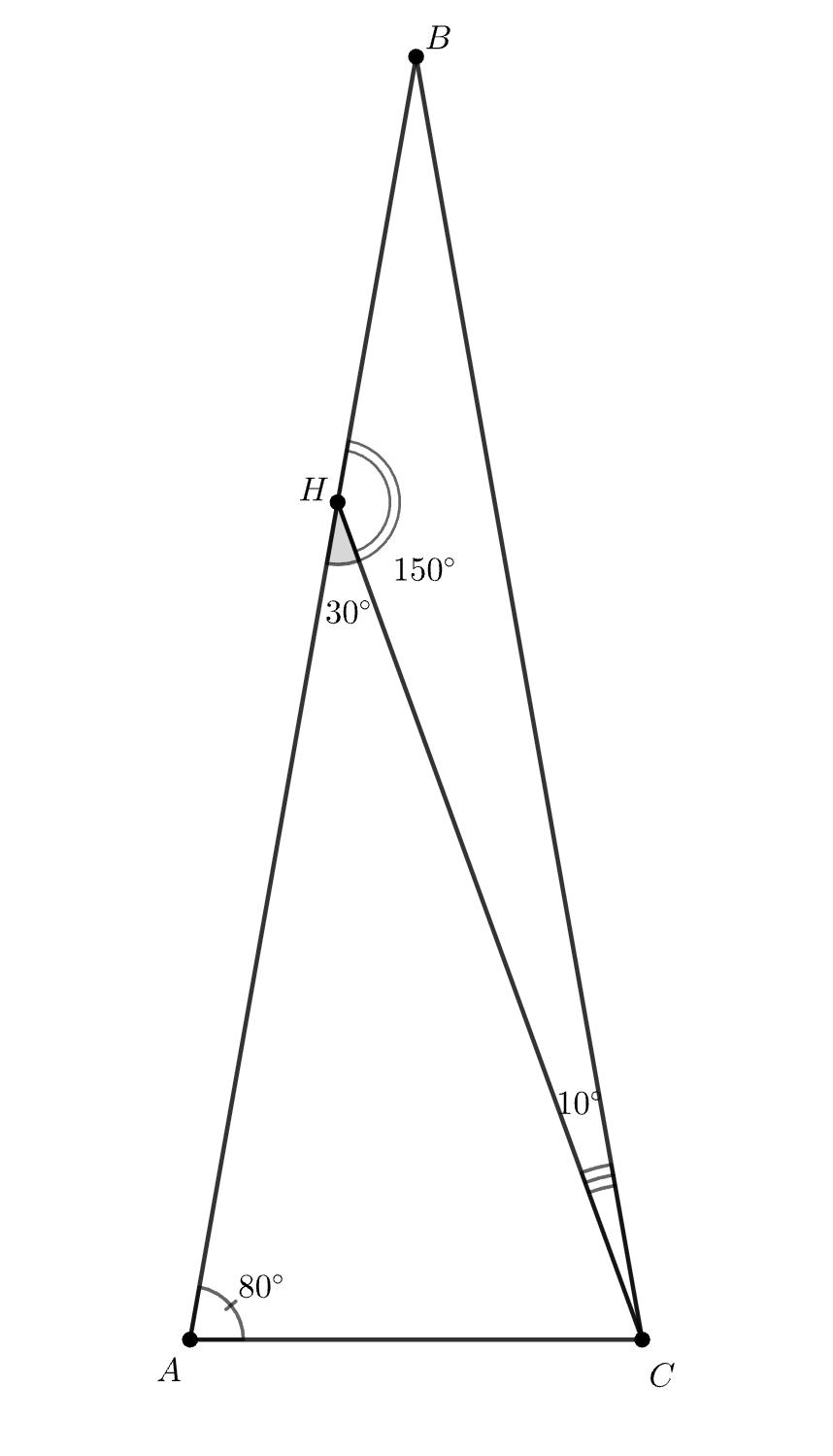
По теореме синусов для треугольника

По теореме синусов для треугольника

Тогда