Поворот
Ошибка.
Попробуйте повторить позже
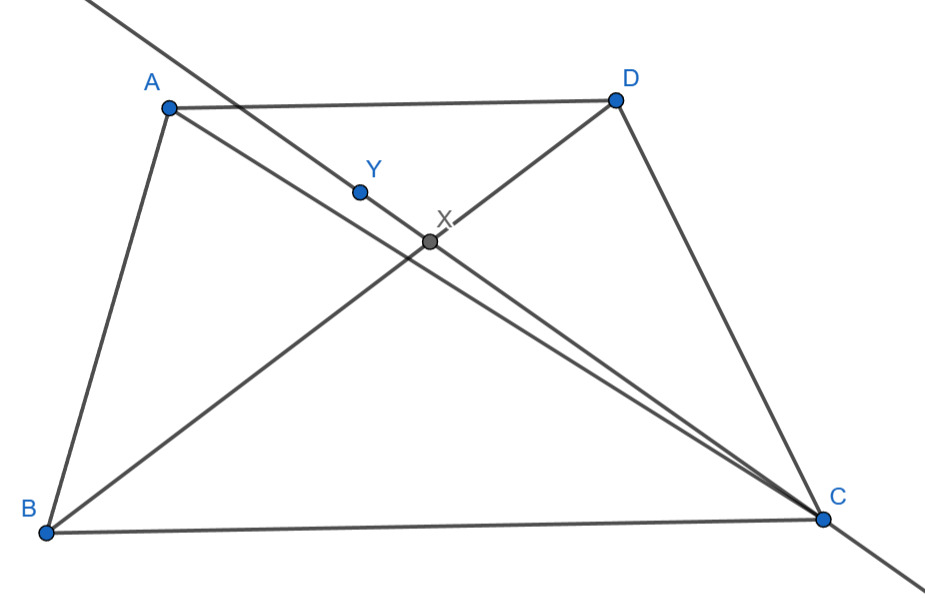
В трапеции длины диагонали
и основания
равны. Точка
на луче
такова, что
На прямой
взята точка
такая, что
Известно, что
(При этом
и
Найдите
градусную меру угла
Источники:
Подсказка 1
Множество равных отрезков да еще и параллельные прямые в трапеции. В такой картинке больше всего хочется найти все равные углы, которые есть, давайте так и поступим.
Подсказка 2
Если вы правильно воспользуетесь равнобедренными треугольниками и параллельностью AD и BC, то станет понятно, что ∠XCB = ∠XDA. Еще мы знаем, что BD = BC, то есть точки D и C находятся как бы на одной окружности с центром в точке B. Что хочется сделать в такой конструкции?
Подсказка 3
Давайте повернем рисунок против часовой стрелки относительно точки B на угол равный альфа. Куда в таком случае перешли точка C и прямая CX?
Подсказка 4
Точка C перейдет в точку D, а прямая CX в прямую AD. Вспомните, что BA=BY, и подумайте, куда в таком случае могла перейти точка Y. Рассмотрите все возможные случаи и найдите в каждом случае градусную меру угла ∠BYC
равнобедренный, поэтому
Накрест лежащие углы равны:
. Значит,
Повернём картинку на угол относительно точки
так, чтобы точка
перешла в точку
Из доказанного выше равенства углов
следует, что прямая
при этом повороте перейдёт в прямую
Точка
при этом перейдёт в такую точку на прямой
что расстояние от неё до точки
равно
Таких точек две. Одна из них точка
а вторая — какая-то точка
Значит, или
как односторонний угол. Это один из
ответов.
Посмотрим теперь на точку
равнобедренный, причём
равен тому из углов
и
который
является острым (случай прямого угла исключается значениями углов
и
которые даны в каждом их вариантов).
Если
тупой, точка
очевидно лежит на луче
и
Если же
острый,
и точка
находится на луче
При этом во всех вариантах
т.е.
поэтому точка
лежит ближе к
чем
, т.е. попадает на отрезок
Значит,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




