Гомотетия
Ошибка.
Попробуйте повторить позже
Вписанная окружность касается сторон треугольника в точках
и
Докажите, что прямая Эйлера треугольника
проходит через центр описанной окружности треугольника
Подсказка 1
Для того, чтобы доказать, что прямая Эйлера треугольника A₁B₁C₁ проходит через О(центр описанной окружности ABC), нужно в явном виде найти эту прямую Эйлера. Для этого, попробуйте опустить высоты в треугольнике A₁B₁C₁ (как минимум одну точку прямой Эйлера мы нашли) и посмотреть на треугольник образованный их основаниями. Что такое Н (ортоцентр A₁B₁C₁) для этого(на основаниях высот) треугольника?
Подсказка 2
Для этого треугольника, который образован основаниями высот в треугольнике A₁B₁C₁, H — инцентр (по свойству ортоцентра). При этом, в силу того, что A₁B₁C₁ — треугольник образованный точками касания вписанной в ABC окружности, AВ-касательная к окружности описанной вокруг A₁B₁C₁. А А₂В₂ — отрезок, соединяющий основания высот. То есть A₂B₂ антипараллельно А1В1, но ведь AB тоже антипараллелен A₁B₁. Значит A₂B₂ || AB. Но ведь так можно сказать и для B₂C₂ и для C₂A₂. Что тогда можно сказать про треугольники ABC и A₂B₂C₂?
Подсказка 3
Верно, они мало того что подобны, но еще и гомотетичны. Так давайте тогда рассмотрим гомотетию, при которой большой треугольник переводится в маленький. Куда тогда переходит H? А что можно сказать насчет того, куда переходит I(центр вписанной окружности)? А что это все дает?
Подсказка 4
А вот, что это дает. Дело в том, что точка, ее образ при гомотетии и центр гомотетии всегда лежат на одной прямой. Пусть центр гомотетии - Х. Точка I-переходит в точку Н, значит точки I,H,X коллинеарны. Точка О же переходит в центр описанной вокруг треугольника A₂B₂C₂ окружности. Значит этот центр, X и О коллинеарны. Из всего нашего набора наиболее непонятен вот этот центр. Что насчет него можно сказать? Чем он является?
Подсказка 5
Поскольку A₂,B₂,C₂ — основания высот, то окружность описанная вокруг A₂B₂C₂ - это окружность Эйлера для треугольника A1B1C1, а значит ее центр лежит на прямой Эйлера, при том эту прямую мы знаем, это прямая HI. Однако, еще и Х лежит на HI, но тогда на этой прямой лежит и центр описанной окружности треугольника A₂B₂C₂, а также точка Х. Значит, на ней лежит и точка О. Что и требовалось доказать!
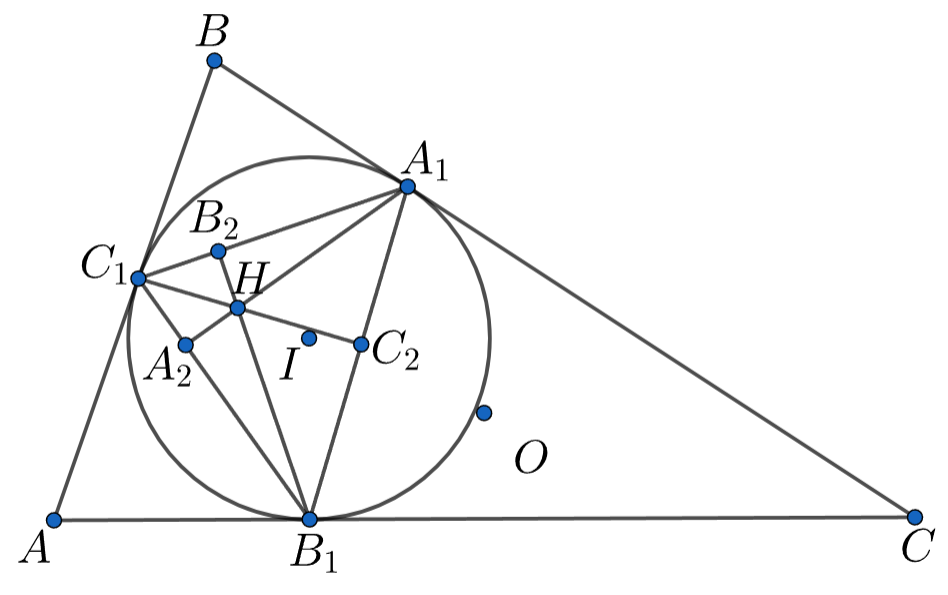
Пусть и
— центры описанной и вписанной окружностей треугольника
— ортоцентр треугольника
Проведем в треугольнике
высоты
и
По свойству ортоцентра
— инцентр треугольника
Стороны исходного треугольника являются касательными к окружности
в соответствующих точках. Каждый отрезок,
соединяющий основания высот
параллелен соответствующей касательной, проведённой к описанной окружности в
соответствующей вершине треугольника (эту несложную лемму можно использовать в данной задаче без доказательства). В итоге стороны
треугольников
и
параллельны.
Значит, существует гомотетия, переводящая треугольник в
При этой гомотетии точка
переходит в точку центр
описанной окружности
а точка
— в точку
Пусть центр гомотетии — некоторая точка тогда тройки точек
центр описанной окружности
и
коллинеарны.
А ведь центр описанной окружности — центр окружности Эйлера для
Значит, он лежит на его прямой Эйлера
Но тогда и
лежит на этой прямой.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




