Поворотная гомотетия

Пусть — данный треугольник, — центр его описанной окружности, — середины его сторон соответственно, так что подобен с коэффициентом и

Пусть при повороте вокруг по часовой стрелке на угол точка переходит в При таком повороте прямая переходит в перпендикуляр к проходящий через пусть этот перпендикуляр пересекает в точке

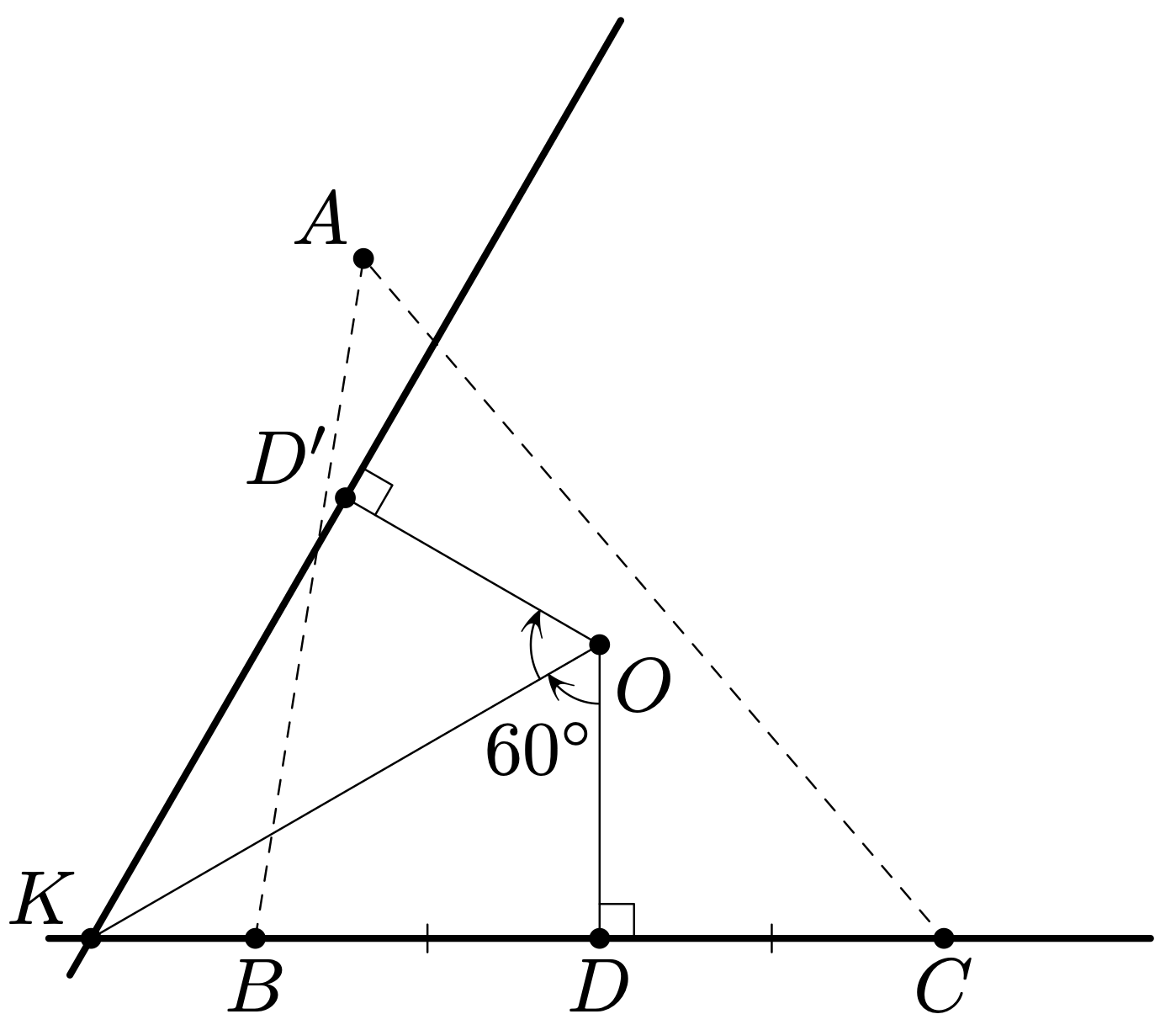
Видим, что прямоугольные треугольники и равны (симметричны относительно ), и поэтому

значит, в прямоугольном треугольнике верно

Иными словами, получается из в результате поворотной гомотетии: поворота с центром по часовой стрелке на угол и последующей гомотетии с центром и коэффициентом Аналогичный результат получим для других точек пересечения одноцветных прямых.

Таким образом, треугольник получается из поворотной гомотетией с центром и коэффициентом Тогда подобен с коэффициентом следовательно, равен