Поворотная гомотетия
Ошибка.
Попробуйте повторить позже
Внутри треугольника 
взята такая точка 
что 
Вне треугольника 
взята такая точка 
что
и точки 
и 
находятся в разных полуплоскостях относительно 
Докажите, что 
где 
—
середина отрезка 
Источники:
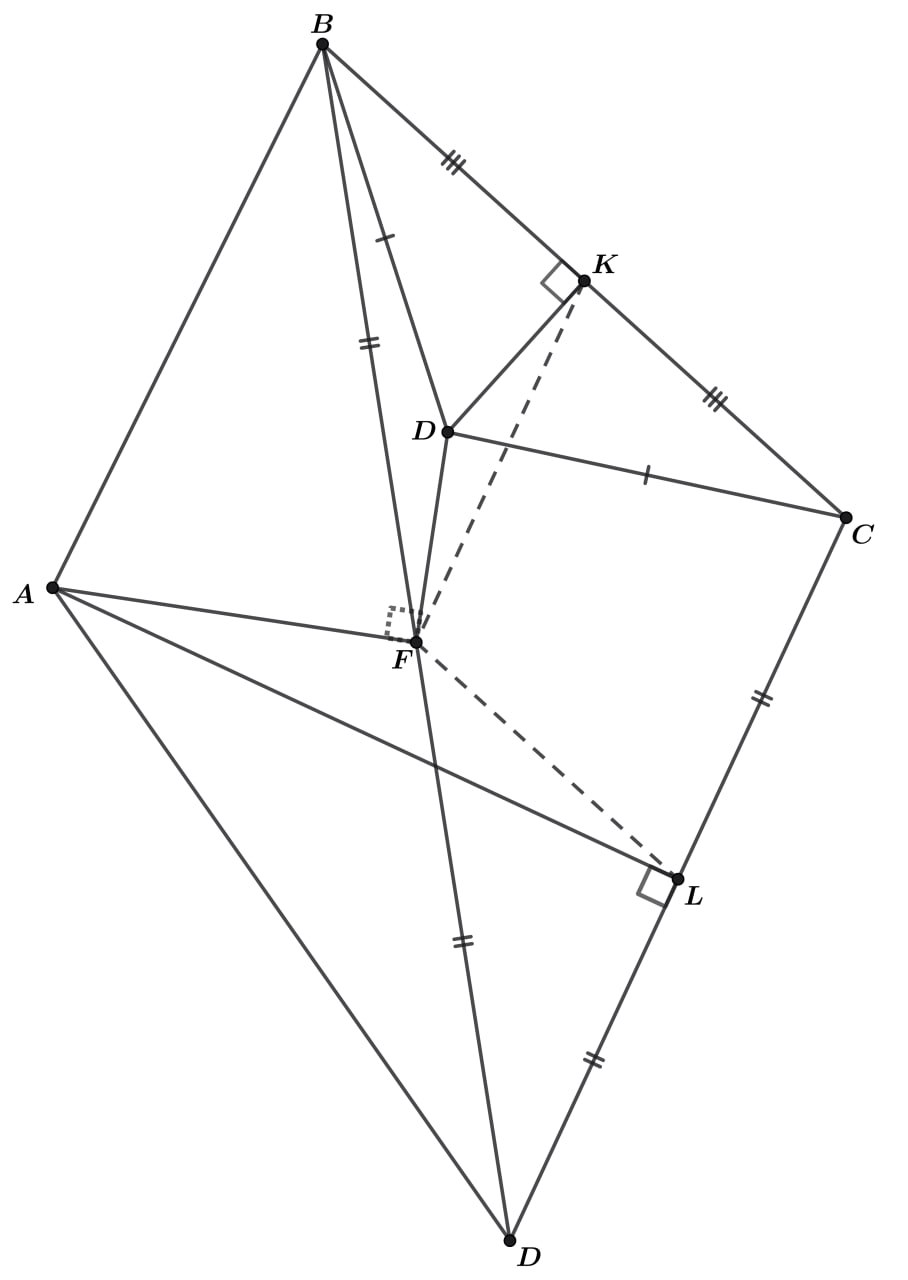
Пусть 
— середины 
соответственно. Отсюда 
и 
— средние линии 
Тогда выполнены равенства 
и
Пусть 
— преобразование на векторах, которое поворачивает вектор на 
против часовой стрелки, а затем увеличивает в
раз. Тогда выполнено
Так как для поворотной гомотетии верно 
то
Откуда и следует нужная перпендикулярность.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
