Инверсия

Первое решение.

Лемма 1. Пусть на сторонах и треугольника взяты точки такие что . Тогда существует окружность, проходящая через и касающаяся одинаковым образом вневписанных окружностей треугольника, вписанных в углы и .

Доказательство. Применим теорему Кези к двум вневписанным окружностям и двум вырожденным окружностям и

______________________________________________________________________________________________________________________________________________________

Лемма 2. Пусть даны две окружности, лежащие одна вне другой. Произвольная окружность, касающаяся их одинаковым образом, пересекает одну из их общих внутренних касательных в точках и а другую — в точках и Тогда среди прямых найдутся две, параллельные общим внешним касательным к данным окружностям.

Доказательство. Действительно, зафиксируем точку на одной из внутренних касательных. Через нее можно провести две окружности, касающиеся данных одинаковым образом. По лемме из теоремы Кези, каждая из этих окружностей проходит через одну из точек пересечения второй внутренней касательной с прямыми, проходящими через и параллельными внешним касательным. Значит, одна из таких точек совпадает, например, с точкой т.е. прямая параллельна одной из общих внешних касательных. Тогда поскольку четырехугольник — вписанный, то прямая параллельна второй внешней касательной.

Вернемся теперь к решению исходной задачи. Очевидно, что окружности и пересекаются. Инверсия с центром в одной из точек их пересечения переводит эти окружности в прямые а исходные концентрические окружности в две окружности, для которых являются общими внутренними касательными. Окружности перейдут в две окружности, касающиеся этих окружностей одинаковым образом. Пусть одна из них пересекает в точках а — в точках . Аналогично вторая окружность пересекает эти прямые в точках . Тогда по лемме получаем, что, например, и, значит, точки лежат на одной окружности. Аналогично доказывается, что остальные четыре точки лежат на одной окружности. Сделав теперь обратную инверсию, получим утверждение задачи.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Обозначим концентрические окружности через и их центр — точки касания с — через точки касания с ними же — через Все углы и дуги предполагаем ориентированными, углы дуги Рассмотрим пару Рассмотрим точку диаметрально противоположную на Тогда

(последнее — т.к. и проходят через Пусть прямые и пересекаются в точке Тогда

т.е. это одна из точек пересечения и Другую точку их пересечения мы обозначим через Заметим, что дуги и окружностей и имеют одинаковую градусную меру, ибо они гомотетичны. Поэтому

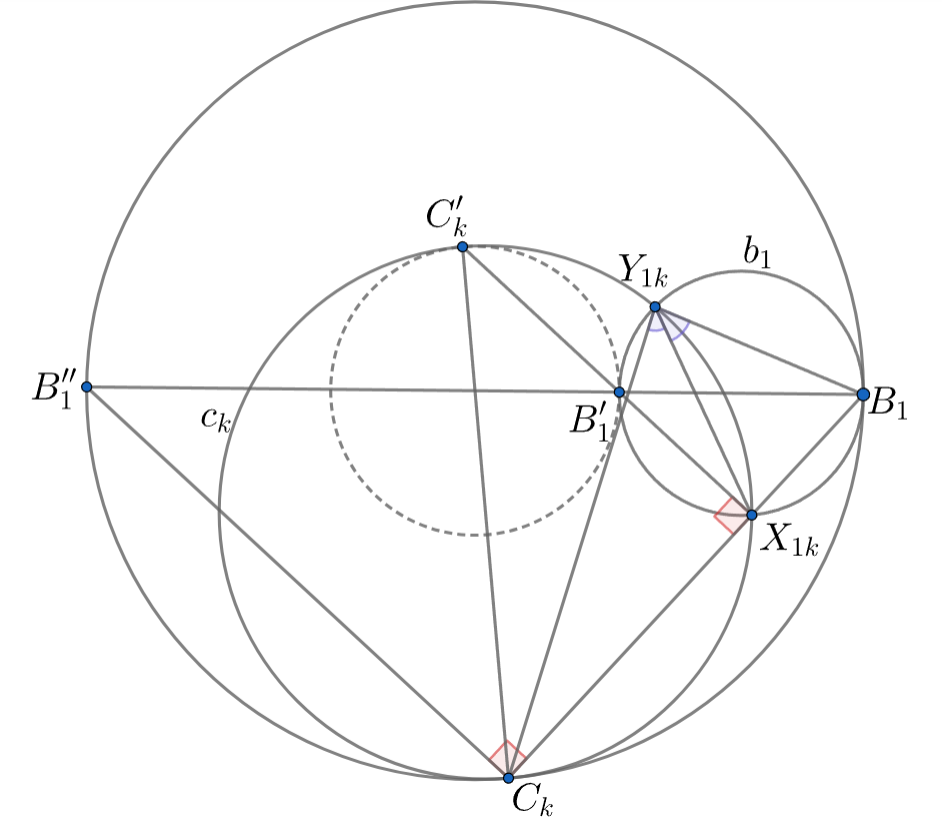
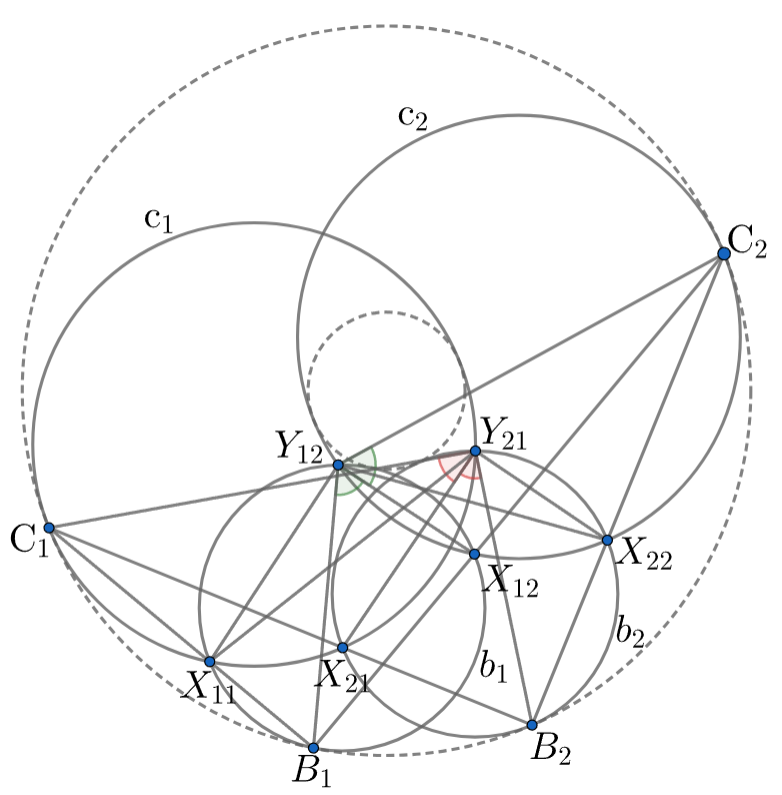
Покажем, что точки и лежат на одной окружности. Имеем

Аналогично,

и

что и требовалось.