Инверсия
Ошибка.
Попробуйте повторить позже
Дан треугольник Окружность
лежит вне треугольника
касается его описанной окружности и отрезка
в точке
Аналогично определяется
Докажите, что если
то одна из общих касательных к
и
параллельна
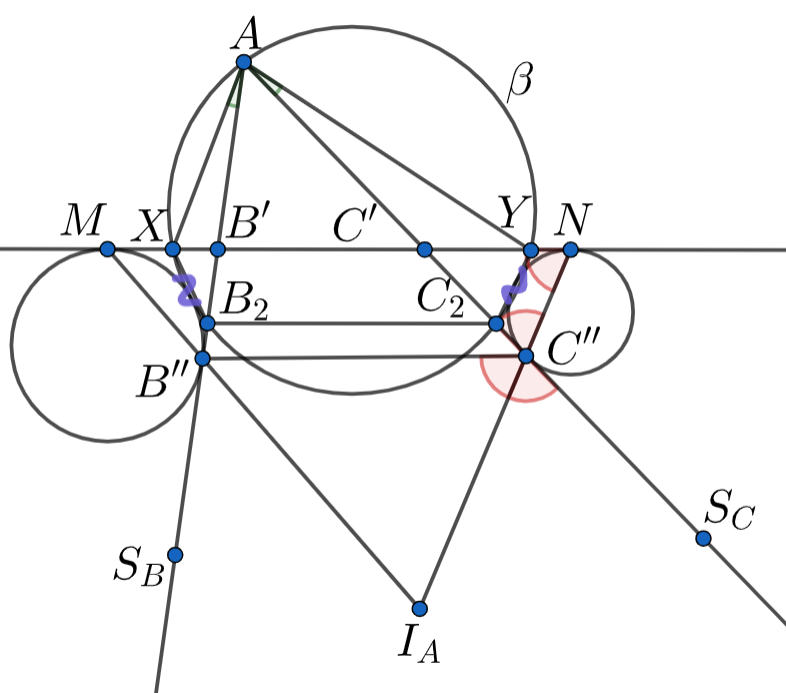
Докажем, что нижняя общая касательная параллельна Сделаем инверсию в точке
с произвольным радиусом. На рисунке образ
любого объекта
обозначается через
Нижняя касательная перейдёт в меньшую окружность (на рисунке обозначим её через
),
проходящую через
и касающуюся
и
поскольку на изначальной картинке она находится дальше от центра инверсии, чем
верхняя общая касательная.
Пусть пересекает
и
в
и
соответственно. Если мы покажем, что
то окружности
и
будут гомотетичны с центром
значит они будут касаться в точке
Но тогда при обратной инверсии мы получим, что
и нижняя общая касательная к
и
параллельны.
Пусть пересекает
в точках
и
Точки касания прямой
с
и
обозначим через
и
соответственно. По внешней лемме Саваямы для
прямые
и
проходят через центр
окружности,
вневписанной в
напротив точки
Прямые
и
параллельны, поскольку их прообразы — касающиеся
в точке
окружности (потому что
). Пусть
Также
поскольку
как отрезки касательных. В силу вертикальности
то есть
— биссектриса
Аналогично доказывается, что
— биссектриса
Следовательно,
также центр вневписанной
окружности
То есть
— биссектриса углов
и
Отсюда получаем, что
а значит
Таким образом,
потому что равные хорды высекаются только параллельными прямыми. Получили
требуемое.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




