Инверсия

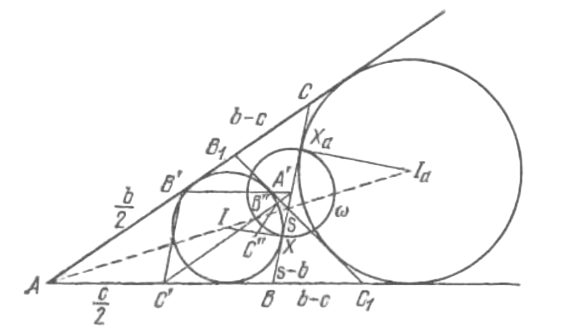
(a) На рисунке изображены треугольник его серединный треугольник окружность, вписанная в треугольник (с центром в точке ), касающаяся стороны в точке одна из вневписанных окружностей (с центром в точке ), касающаяся стороны в точке и общая касательная к этим двум окружностям (которые одновременно касаются всех трех сторон треугольника ). На этом рисунке также изображены окружность построенная на отрезке как на диаметре, и точки в которых отрезок пересекает отрезки Так как окружность ортогональна к вписанной и к вневписанной окружностям, то при инверсии относительно окружности обе эти окружности переходят в себя. Теперь мы переходим к доказательству того, что инверсия относительно окружности переводит окружность девяти точек в прямую

Известно, что длина и равна где откуда следует, что центром окружности является точка — середина отрезка а длина диаметра окружности равна

(эту величину мы предполагаем положительной; в противном случае проведем те же построения по отношению к другой стороне, соответственно переименовав вершины ). Окружность девяти точек проходит через точку — центр окружности следовательно, при инверсии относительно окружности она переходит в прямую. Показав, что точки и являются образами при инверсии относительно окружности точек и лежащих на окружности девяти точек, мы получим, что эта прямая проходит через точки и (а поэтому и через точки и ).

Так как точка (так же как и точки и ) лежит на биссектрисе угла а известно, что делит отрезок (длины ) в отношении то мы имеем

и полуразность этих двух длин равна

Также и, аналогично,

Так как треугольник подобен треугольнику и треугольник подобен треугольнику то мы имеем

и

и

Таким образом, при инверсии относительно окружности радиус которой равен точка переходит в точку а точка — в точку что и требовалось.

Более того, инверсия относительно окружности переводит вписанную окружность и рассмотренную вневписанную окружность в самих себя, а их общую касательную в окружность девяти точек. Следовательно, окружность девяти точек, как и прямая касается этих двух окружностей. Аналогично, с помощью инверсии в точках и мы получим касание окружности Эйлера с другими вневписанными окружностями.

_________________________________________________________________________________________________________________________________________________________________________________

(b) Достаточно показать, что точки и (точка касания окружности Эйлера и вневписанной окружности, соответствующей вершине ) лежат на одной прямой. Тогда, аналогично, и тоже лежат на одной прямой. Все невведённые обозначения взяты из прошлого пункта. Вспомним инверсию, которая использовалась для доказательства теоремы Фейербаха. Напомним, что ее центр это а радиус – Достаточно доказать, что точки лежат на одной окружности, где объект со звездочкой это образ точки под действием описанной инверсии. Точки и могут быть определены как образы точек касания вписанной и вневписанной окружности со стороной (она образуется при симметрии относительно биссектрисы треугольника — это тоже было в доказательстве пункта выше).

Пусть и Ясно, что Также, поэтому

Пусть — точка касания вневписанной окружности со стороной Тогда

Воспользуемся свойством степени точки. Поскольку прямые и пересекаются в точке то для того, чтобы установить, что лежат на одной окружности, достаточно доказать, что Из симметрии касающейся прямой мы получаем, что и Также можем заменить на из свойств инверсии. Итак, нужно доказать тождество

Преобразуем левую часть

Теперь раскроем слева скобки

Видно, что одно из слагаемых слева сократится, и мы получим два одинаковых выражения. Победа!