Инверсия
Ошибка.
Попробуйте повторить позже
Зафиксируем окружность прямую
касающуюся
и еще одну окружность
не имеющую общих точек с
такую, что
и
лежат по разные стороны от
Касательные к
из переменной точки
лежащей на окружности
пересекают прямую
в точках
и
Докажите, что когда
пробегает
описанная окружность треугольника
касается двух фиксированных
окружностей.
Не умаляя общности положим, что имеет единичный радиус. Пусть точка
— центр
Сделаем инверсию в точке
с радиусом
Все касательные при инверсии перешли в окружности единичного диаметра, касающиеся
внутренним образом. После инверсии задача
звучит следующим образом:
Зафиксируем окружность единичного радиуса, окружность
единичного диаметра, касающуюся
внутренним образом, а также
окружность
внутри
Окружности
и
единичного диаметра также касаются
внутренним образом, пересекаются в точке
на
окружности
пересекают
в точках
и
соответственно. Докажите, что когда
пробегает
окружность
касается двух
фиксированных окружностей.
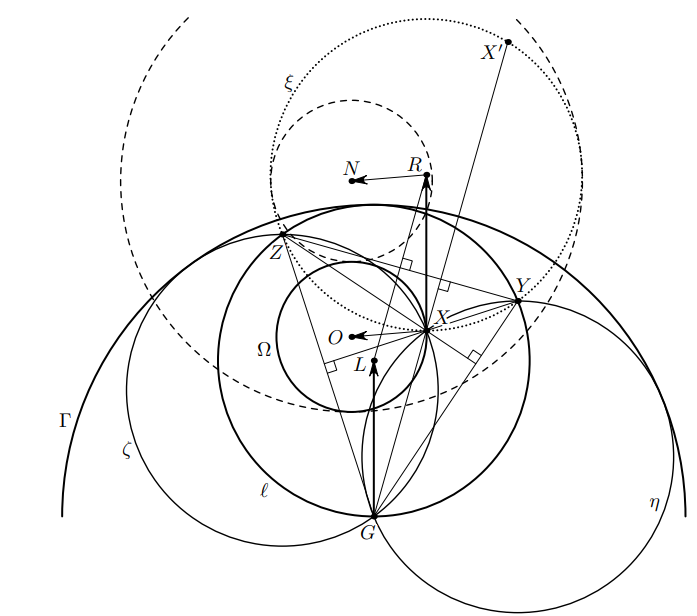
Поскольку и
являются отражениями описанной окружности треугольника
относительно сторон
и
соответственно,
они проходят через ортоцентр этого треугольника. Эти окружности пересекаются в точке
Значит, она и является ортоцентром
треугольника
Следовательно, окружность
также является отражением окружности
относительно
Пусть точки и
— центры
и
соответственно, а точка
— центр
Пусть
пересекает вторично
в точке
Точки
и
симметричны относительно прямой
, откуда
равнобокая трапеция. Значит,
Также
имеем
откуда Это означает, что
то есть равенство
верно независимо от выбора точки
Наконец, определим фиксированную точку такую, что
Четырёхугольник
— параллелограмм, значит равенство
верно независимо от выбора
Следовательно,
касается фиксированных окружностей с центром в точке
и
радиусами
и
Осталось проверить, что при обратой инверсии найденые окружности не перейдут в прямые. Это может случиться, если какая-то из них
проходит через Покажем, что это невозможно. Действительно, поскольку
лежит внутри
имеем
откуда
Это доказывает, что находится всне рассматриваемых окружностей.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




