Считаем рёбра
Ошибка.
Попробуйте повторить позже
Предложите эффективный алгоритм для поиска максимального потока в графе с целочисленными весами, используя теорему Форда-Фалкерсона. Обоснуйте его корректность. Будет ли ваш алгоритм работать для вещественных весов?
Алгоритм Эдмондса-Карпа с обходом в ширину
Шаги алгоритма:
- 1.
-
Инициализация: поток
для всех рёбер.
- 2.
-
Пока существует путь из истока
в сток
в остаточной сети
- Найти кратчайший путь
из
в
с помощью BFS (обход в ширину).
- Увеличить поток вдоль
на величину остаточной пропускной способности
- Обновить остаточную сеть
- Найти кратчайший путь
Корректность:
- Теорема Форда-Фалкерсона: Поток максимален тогда и только тогда, когда в остаточной сети нет дополняющих путей, значит, пока поток не максимален, найдется путь, по которому мы увеличим поток.
- Конечность: При целочисленных пропускных способностях каждый шаг увеличивает поток на целое число. Так как
максимальный поток ограничен (например, суммой пропускных способностей рёбер из истока), алгоритм завершится за
шагов, где
— значение максимального потока, и на каждом шаге мы заупскаем BFS.
Пример несходящегося алгоритма: Рассмотрим сеть с источником стоком
рёбрами
и пропускными
способностями:
а пропускные способности остальных рёбер равны целому числу
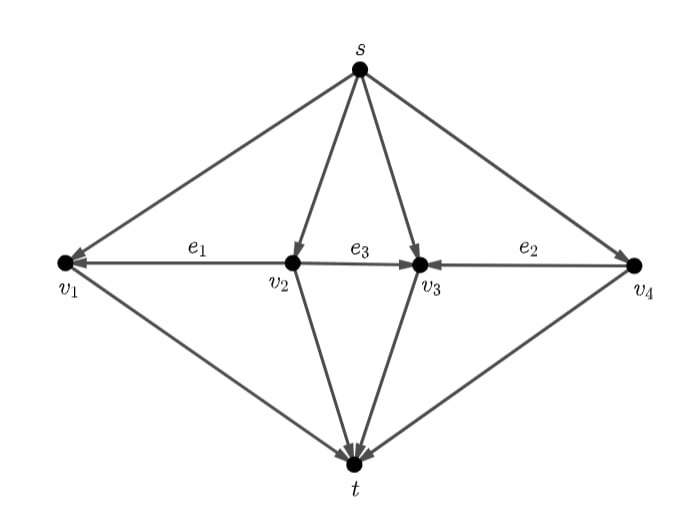
Константа удовлетворяет условию:
Используем пути в остаточном графе:
| Шаг | Найденный путь | Добавленный поток | | | |
| 0 | — | — | | | |
| 1 | | 1 | | | |
| 2 | | | | | 0 |
| 3 | | | | | |
| 4 | | | | 0 | |
| 5 | | | | | |
- После шагов
и
остаточные пропускные способности рёбер
имеют вид
где
-
Цикл из путей
может повторяться бесконечно. Полный поток после шага
-
При бесконечном выполнении поток сходится к:
но максимальный поток равен
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




