Считаем рёбра
Ошибка.
Попробуйте повторить позже
В углах доски стоят кони: по
коня черного и белого цветов, причем кони одного цвета стоят в противоположных углах. За один
ход разрешается выбрать любого коня и сделать им ход в свободную клетку. Можно ли переставить коней так, чтобы по прежнему все кони
стояли в углах, но кони одного цвета стояли в углах при одной стороне?
Подсказка 1
Попробуем перевести задачу на язык графов. Что можно считать ребрами, а что вершинами?
Подсказка 2
Верно! Клетки будут вершинами, а ребра будут между теми клетками, которые соединены одним ходом коня. А можно ли этот граф перерисовать более удобно?
Подсказка 3
Верно! Можно перерисовать граф так, чтобы ребра не пересекались. Какой тогда можно увидеть инвариант для коней?
Подсказка 4
Заметим, что кони не перепрыгивают через вершины графа и могут передвигаться только по ребрам. Какой тогда получается инвариант?
Нарисуем граф коня на этой доске, то есть соединим ребрами клетки, соединенные одним ходом коня. Для этого отметим вершину графа в
центре каждой клетки, назвав их для удобства
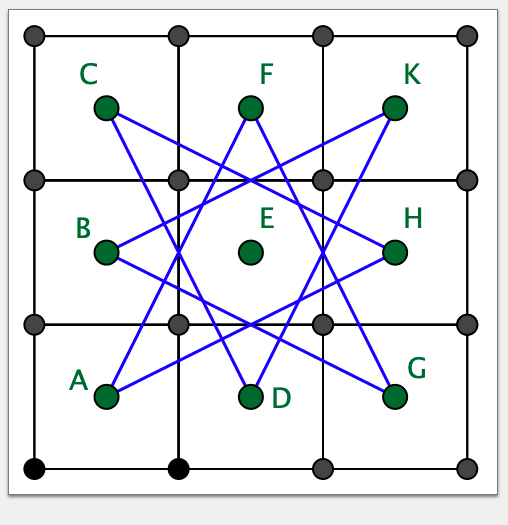
Перерисуем этот граф для удобства так, чтобы ребра не пересекались.
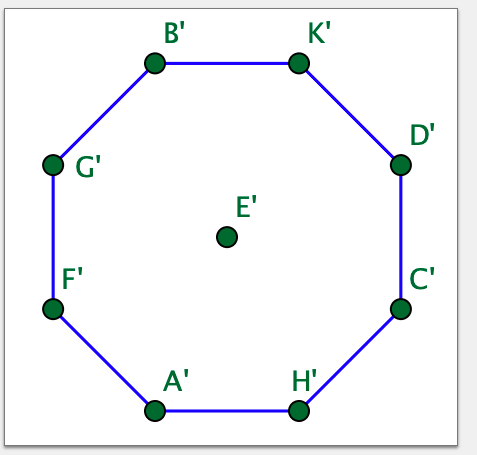
По условию, изначально кони стоят в углах, то есть в вершинах и
Пусть не умаляя общности белые кони стоят в вершинах
и
а черные — в
и
Заметим, что кони могут передвигаться из вершины в вершину только по ребрам. При этом перепрыгивать через вершины они не могут. Значит, порядок коней в этом круге измениться не может. Изначально кони стоят в порядке Белый-Черный-Белый-Черный. Если бы кони одного цвета могли встать в соседних углах, то получился бы порядок Белый-Белый-Черный-Черный. Это, как мы только что выяснили, невозможно, поэтому ответ в задаче — нет, нельзя.
Нет, нельзя
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




