Гуляем по графу
Ошибка.
Попробуйте повторить позже
Пусть — два множества вершин в ориентированном (возможно, с кратными ребрами и петлями) конечном графе
Назовем
множество
хорошим, если из
в
существует |
| непересекающихся по вершинам путей. Докажите, что все максимальные по
включению хорошие множества содержат одинаковое количество элементов.
Подсказка 1
Будем идти от противного. Пусть найдутся такие множества C и D ∈A, что |C| < |D|. Пусть P и Q — множество непересекающихся путей из C и D соответственно в B. P и Q состоят из путей P_i и Q_i. Попробуйте доказать, что путь Q_i не может не пересекать пути из P.
Подсказка 2
Теперь будем пытаться перестраивать пути так, чтоб в D образовалась вершина, путь из которой не пересекает пути из C. Давайте рассмотрим путь Q_i, конец которого не будет концом путей из P. А почему такая есть?
Подсказка 3
Правильно! В силу того, что |C| < |D|. Будем рассматривать пути P_j такие, что общая вершина P_j и Q_i была самой близкой к концу Q_i. И будем менять часть пути P_j на часть пути из Q_i, которая идет после общей вершины. Что тогда останется верным про пути из P?
Подсказка 4
Верно! Они до сих пор не пересекаются! Теперь хочется доказать, что этот алгоритм закончиться как нам надо. Для этого рассмотрим две величины. S_P(n) — число всех ребер в путях из P на шаге n данного алгоритма. S_Q(n) — число общих ребер в путях из P и Q на шаге n данного алгоритма. Какую еще величину (от этих двух) стоит рассмотреть?
Подсказка 5
Ага! Рассмотрим S(n) равной разности S_p(n) и S_q(n). Что тогда можно сказать просто по определению S_p(n) и S_q(n) про S(n)?
Подсказка 6
Точно! S(n) ≥ 0. Теперь вспомним, что делает наш алгоритм и что мы хотим доказать, что он закончится. Что еще можно сказать про S(n)?
Подсказка 7
Верно! S(n) > S(n + 1). А значит наш алгоритм придет к тому, что S(n) = 0. Осталось только понять, что это значит.
Пусть существуют два хороших хороших множества которые содержат различное количество элементов. Без ограничений
общности считаем, что
Покажем, что не является максимальным по включению.
Действительно, пусть и
— множество непересекающихся путей из
и
соответственно в
Если
существует путь
который не пересекается с любым путем из
то мы можем добавить его начало в
следовательно,
не является максимальным по включению. Далее считаем, что все пути из
пересекаются какими-либо путями из
Рассмотрим следующий алгоритм перестройки путей и покажем, что рано или поздно в образуется вершина, путь из которой не
пересекается с любым из путей из вершин
Поскольку
найдется путь
конец которого не является концом никакого пути
из
и
пересекается с некоторым подмножеством путей из
Пусть
тот из них, для которого общая вершина с
наиболее близка к концу
(рис.
ребра
покрашены в красный,
— в синий). Заменим часть пути
на часть пути из
которая идет после общей вершины. Тогда в
по прежнему никакие два пути не пересекаются
(рис.
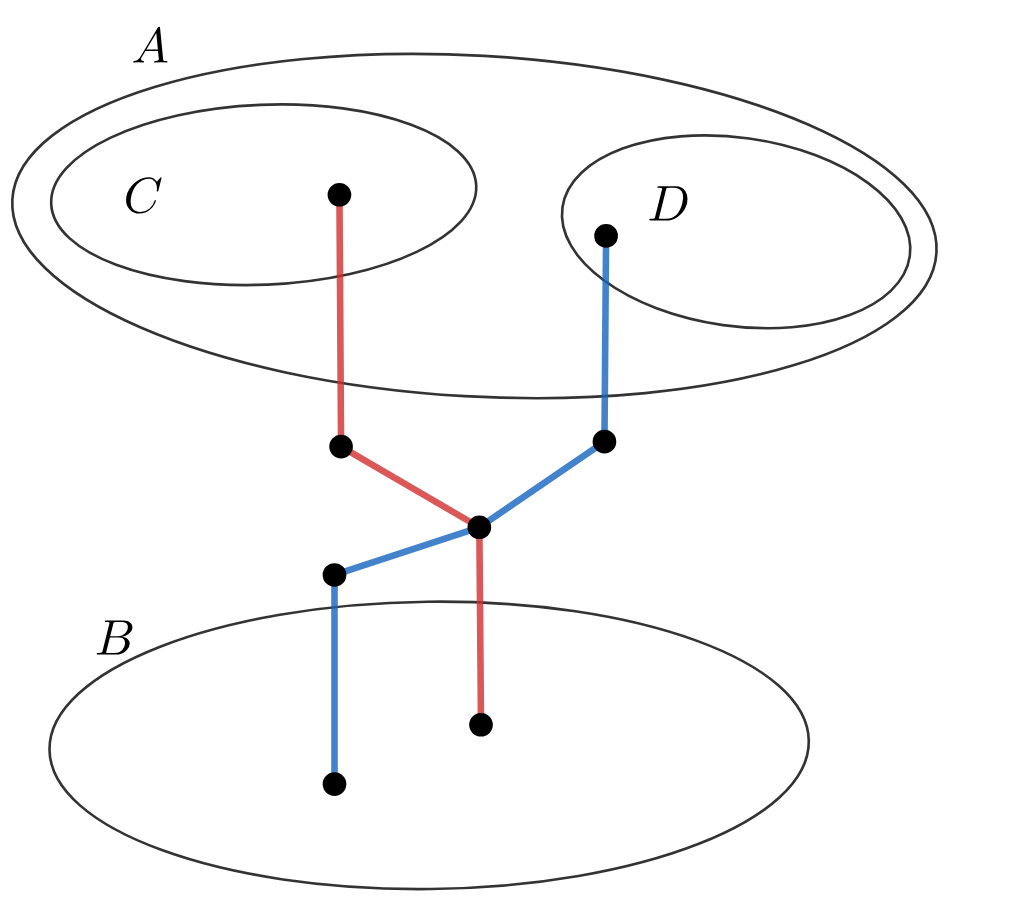
Рис.1
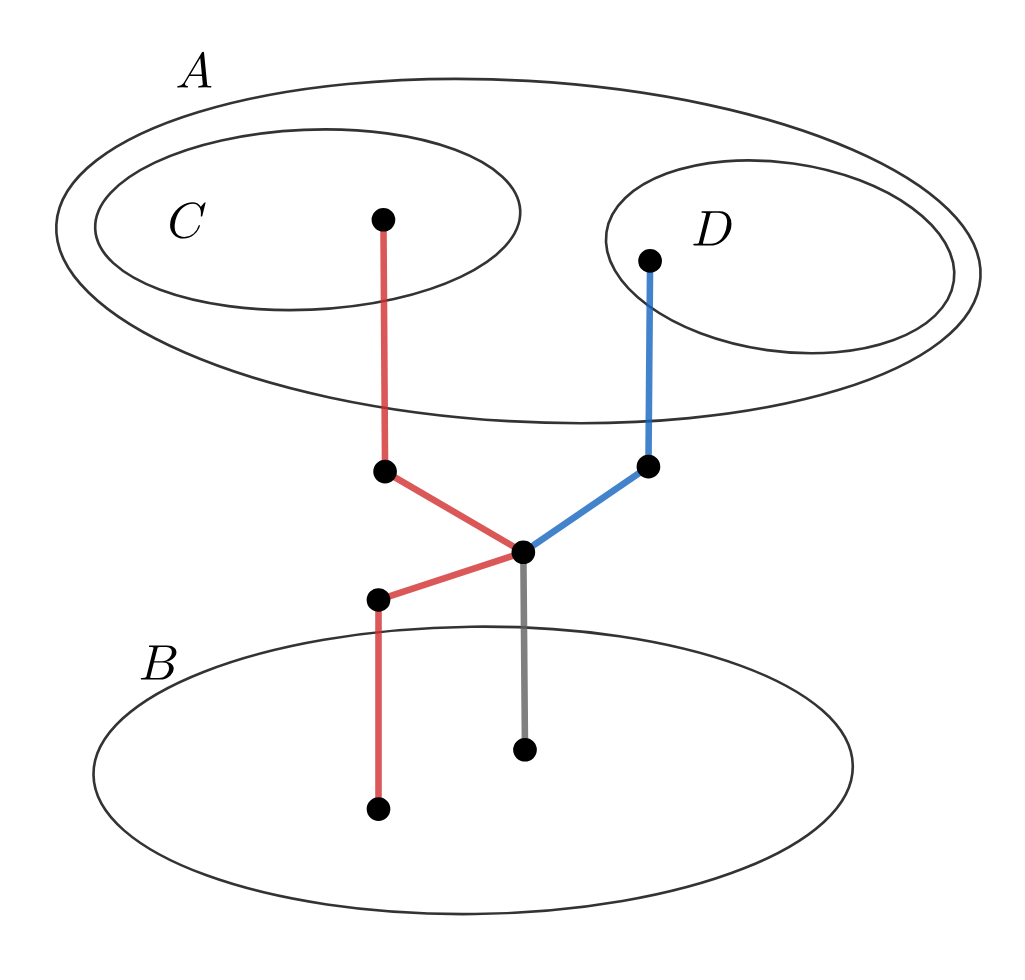
Рис.2
Пусть — число всех ребер в путях из
на шаге
данного алгоритма,
— число общих ребер в путях из
и
на
шаге
данного алгоритма. Рассмотрим величину
на шаге данного алгоритма. Поскольку количество общих ребер увеличивается на число большее, чем количество ребер в
перестраиваемом пути
Таким образом, мы можем совершать шаг алгоритма каждый раз, пока существует путь из который пересекается с каким-то путем
из
и не имеет общий конец с любым путем в
но
по определению, то есть рано или поздно все пути из
таковы,
что удовлетворяют ровно одному из условий
- 1.
-
имеют общий конец с каким-то путем из
- 2.
-
не имеют общих вершин с любым путем из
но все пути не могут удовлетворять
поскольку
поэтому найдется путь, который удовлетворяет
— его начало можно
добавить в
а, значит,
не является максимальным по включению.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




