Неравенство ломаной
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Дан выпуклый многогранник. Разделим длину каждого ребра на сумму длин остальных ребер и вычислим сумму полученных дробей.
Докажите, что полученная сумма меньше
Источники:
Подсказка 1
В плоскости мы умеем давать оценки на какие-то суммы длин. Но сейчас мы работаем в пространстве, значит, нужно найти плоскости!
Подсказка 2
Рассмотрите многоугольники, в которые входит конкретное ребро. Какие оценки на длину этого ребра можно в них сделать?
Подсказка 3
Воспользуйтесь неравенством многоугольника для каждого ребра!
Подсказка 4
Для каждого ребра имеется как минимум два непересекающихся набора других рёбер, длины которых в сумме больше, чем длина этого ребра. Тогда можно сделать оценку на длину каждого ребра многогранника!
Подсказка 5
Длина ребра многогранника всегда меньше, чем L/3, где L — сумма длин рёбер многогранника.
Обозначим за длины ребер многогранника, а за
— сумму длин всех ребер многогранника. Каждое ребро многогранника
входит в две грани, которые являются многоугольниками. Отсюда следует, что для каждого ребра имеется как минимум два
непересекающихся набора других ребер, длины которых в сумме больше, чем длина этого ребра (по неравенству многоугольника). Это
значит, что длина каждого ребра многогранника всегда меньше, чем
а значит, сумма длин всех ребер, кроме одного, всегда больше,
чем
Теперь запишем сумму дробей из условия и заменим в каждой дроби знаменатель на
— от этого сумма строго увеличится,
но станет равной
Ошибка.
Попробуйте повторить позже
Дан шестиугольник в котором
Докажите, что
Источники:
Подсказка 1
Вспомним условие на сумму углов в n-угольнике. Чем нам это может помочь? Для каких углов получается выразить величины?
Подсказка 2
Обратим внимание на четырёхугольник, образованный точками A, B, D, E. Какие свойства есть у вписанного четырёхугольника? Что ещё можно сказать про этот четырёхугольник?
Подсказка 3
Попробуем применить симметрию относительно середины отрезков BD и AE – какие новые точки и фигуры при этом получаются?
Подсказка 4
Рассмотрим полученные после отражения точки и параллелограммы. Какие стороны оказываются параллельны, а какие равны по длине? Можно ли использовать равенство углов и расстояний до прямой, чтобы сделать вывод о равенстве боковых сторон и параллельности оснований новой фигуры?
Подсказка 5
Вспомним, что средняя линия трапеции меньше её диагонали. Как это поможет доказать, что равенство возможно только в вырожденном случае?
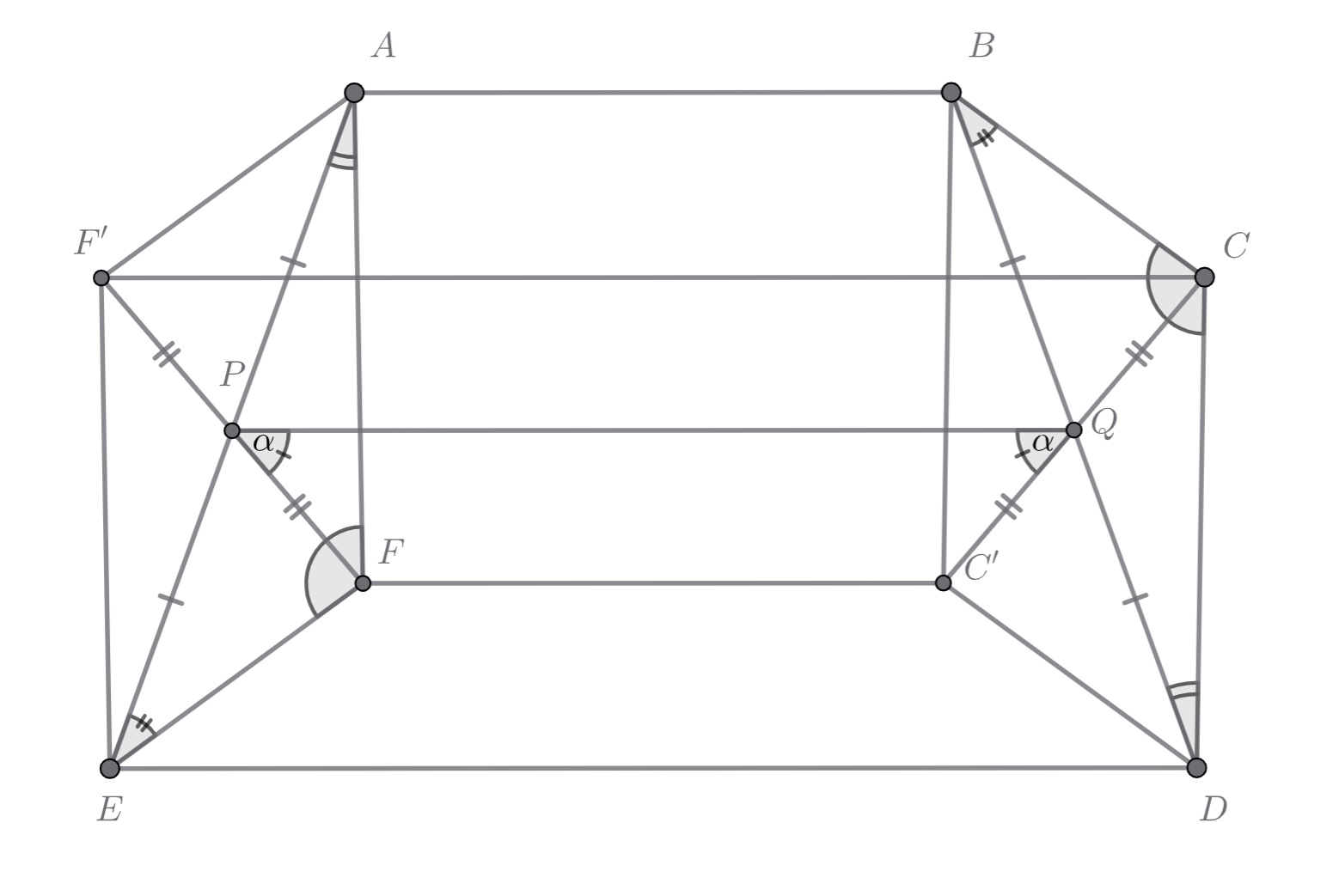
Так как сумма любого -угольника равна
то сумма углов любого шестиугольника, не обязательно выпуклого, равна
Поэтому из условия
следует, что
что, в свою очередь, влечет равенство треугольников
и
по двум сторонам и углу между ними. Так как углы
и
равны, а
четырехугольник
— вписанный. Хорды
и
его описанной окружности равны, поэтому
является равнобокой
трапецией.
Пусть, без ограничения общности, Отразим точки
и
относительно середин
и
отрезков
и
соответственно, получим точки
и
Параллелограммы
и
равны, поэтому
Отсюда делаем вывод, что Расстояние от точки
до прямой
равно
что равно
расстоянию от точки
до прямой
На то же расстояние удалены точки
и
от прямой
поэтому четырехугольник
является равнобокой трапецией с основаниями
и
параллельными прямой
(и, соответственно,
и
).
Кроме того, отрезок
является общей средней линией для трапеций
и
и его длина равна
Но в
отрезок
является диагональю, которая всегда длиннее, чем средняя линия, если трапеция невырождена.
Равенство
возможно только если
и
обе попали на прямую
и
является вырожденной
трапецией.
Ошибка.
Попробуйте повторить позже
В пространстве даны скрещивающиеся перпендикулярные прямые и
Точки
и
— середины отрезков
и
соответственно. Докажите, что
Источники:
Подсказка 1:
Давайте перенесём EF в левую часть неравенства и будем доказывать в таком формате. Попробуйте ввести некоторые обозначения, чтобы левую часть неравенства можно было записать в более удобном виде.
Подсказка 2:
Деление на 2 намекает, что стоит обозначить через M и N середины AD и BC.
Подсказка 3:
Обратите внимание на четырехугольник MENF. Что про него можно сказать? Не забывайте про перпендикулярность из условия.
Подсказка 4:
MENF — прямоугольник. Используя это, попробуйте превратить левую часть неравенства в сумму звеньев ломаной, которая начинается и заканчивается в BD.
Подсказка 5:
Не забывайте, у прямоугольника диагонали равны.
Обозначим через и
середины отрезков
и
Тогда
— средняя линия в треугольнике
а
— в
треугольнике
Следовательно,
Аналогично
Таким образом, точки
лежат в одной
плоскости, причём из условия
следует, что
— прямоугольник. Значит, равны его диагонали
и
Заметим, что
по неравенству ломаной, остаётся вычесть из обеих частей.
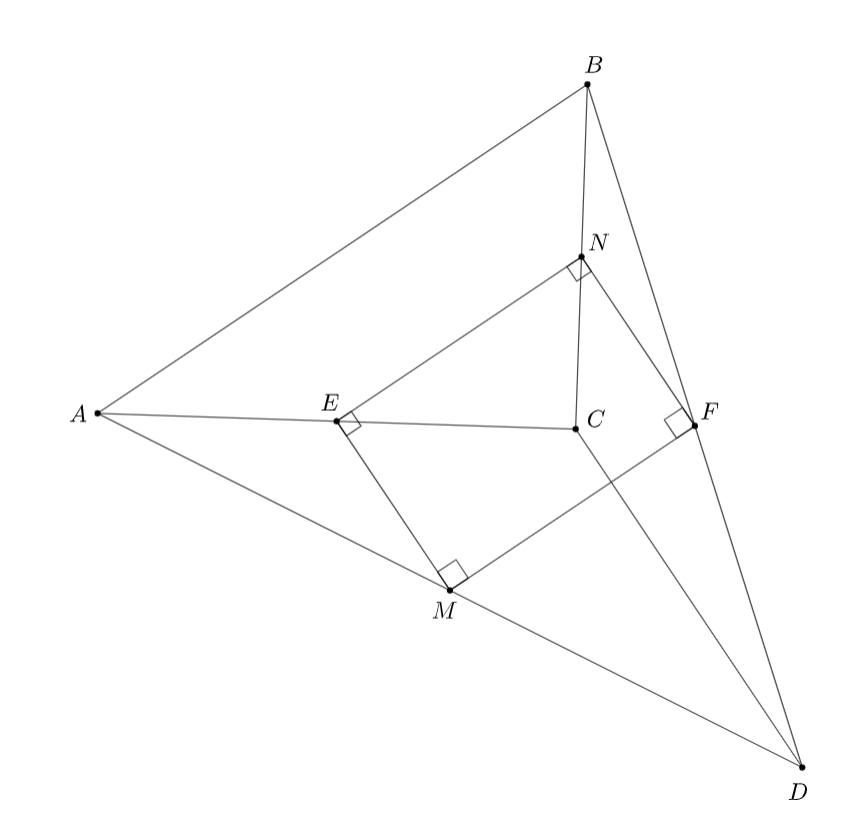
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике углы
и
— тупые. На сторонах
,
,
и
отмечены точки
,
,
и
соответственно. Докажите, что периметр четырёхугольника
больше удвоенной длины диагонали
.
Начертим четырёхугольник симметричный четырёхугольнику
относительно точки
и отметим соответствующие
точки
и
Заметим, что
так как
— тупой по условию, а
- середина отрезка
то есть
находится в той же полуплоскости относительно серединного перпендикуляра к
что и точка
Также заметим, что так как
симметричен
относительно точки
то
Далее продлим
на свою длину — точка
Отметим
на
точку
так, что
![]()
Аналогично отрезкам можем получить, что
(так как
- тупой по условию). Так
как
и
(
— параллелограмм). Таким образом, для пятиугольника
можем выписать неравенство:
Так как получаем, что:
Значит,
Ошибка.
Попробуйте повторить позже
Точка лежит внутри острого угла. Постройте на сторонах этого угла точки
и
, для которых периметр треугольника
был
бы наименьшим.
Обозначим вершину угла через . Отразим точку
относительно сторон угла, обозначив полученные две точки через
и
.
![]()
Рассмотрим произвольные точки и
на сторонах угла. Заметим, что в силу симметрии
,
. Поэтому
периметр треугольника
равен длине ломаной
. Длина этой ломаной не меньше длины отрезка
, и
равенство возможно только когда точки
и
лежат на отрезке
. Поэтому в качестве точек
и
таких,
чтобы периметр треугольника
был наименьшим, необходимо выбрать точки пересечения отрезка
со сторонами
угла.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание.
Условие, что исходный угол острый, важно: если бы был тупым, то построенный отрезок
не пересекался бы со сторонами угла,
а если бы
был прямым, то пересекался бы в точке
. В качестве упражнения докажите, что в обоих этих случаях в качестве точек
и
необходимо выбрать точку
, таким образом, периметр вырожденного треугольника
является наименьшим из
возможных.
Ошибка.
Попробуйте повторить позже
В четырёхугольнике углы
и
— не острые. На сторонах
и
отмечены точки
и
соответственно.
Докажите, что периметр четырёхугольника
не меньше удвоенной длины диагонали
Подсказка 1
Попробуем доказать, что отрезок, соединяющий середины противоположных сторон, не больше полусуммы противоположных сторон!
Подсказка 2
Оценивать длины отрезков, пересекающих AC, сложно. Поэтому попробуем использовать доказанное неравенство, отметим середины противоположных сторон во внутреннем четырехугольнике.
Подсказка 3
Попробуем использовать то, что углы A и C - не острые. Если P и Q - середины сторон KN и LM, то что можно сказать о длинах AP и CQ?
Подсказка 4
Длина медианы, проведенной из вершины при неостром угле, не превосходит половины стороны, к которой она проведена! Значит, мы можем оценить AP и CQ, а после - использовать неравенство ломаной, чтобы оценить AC!
Лемма. Пусть и
— середины сторон
и
четырехугольника
. Тогда
Доказательство. Пусть — середина диагонали
Тогда
![]()
По неравенству треугольника для треугольника имеем:
после подстановки полученных равенств:
что завершает доказательство.
Вернемся к решению задачи. Пусть и
— середины сторон
и
![]()
По лемме Ясно, что длина медианы, проведенной из вершины при неостром угле, не превосходит половины
стороны, к котором она проведена, следовательно
и
Осталось заметить, что по неравенству ломанной верно
неравенство
Подставляя полученные неравенства имеем
домножив данное неравенство на получим требуемое.
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике
и
Докажите, что
.
Подсказка 1
Угол в 20 градусов — так себе угол, нам больше нравятся углы в 30, 45, 60 или 90 градусов.. Как бы из угла 20 градусов сделать один из этих углов?
Подсказка 2
Давайте попробуем сделать угол в 60 градусов! Для этого отсимметричим треугольник АВС относительно ВС, а потом еще раз, относительно новой полученной стороны! Вспоминаем, что известно про треугольники с углом 60
Подсказка 3
Хм, теперь из оснований равнобедренного треугольника образовалась ломаная! Что бы с ней сделать...
Повернём вокруг точки
против часовой стрелки на 20 градусов, получим
. Сделаем такой же поворот для
,
получим
.
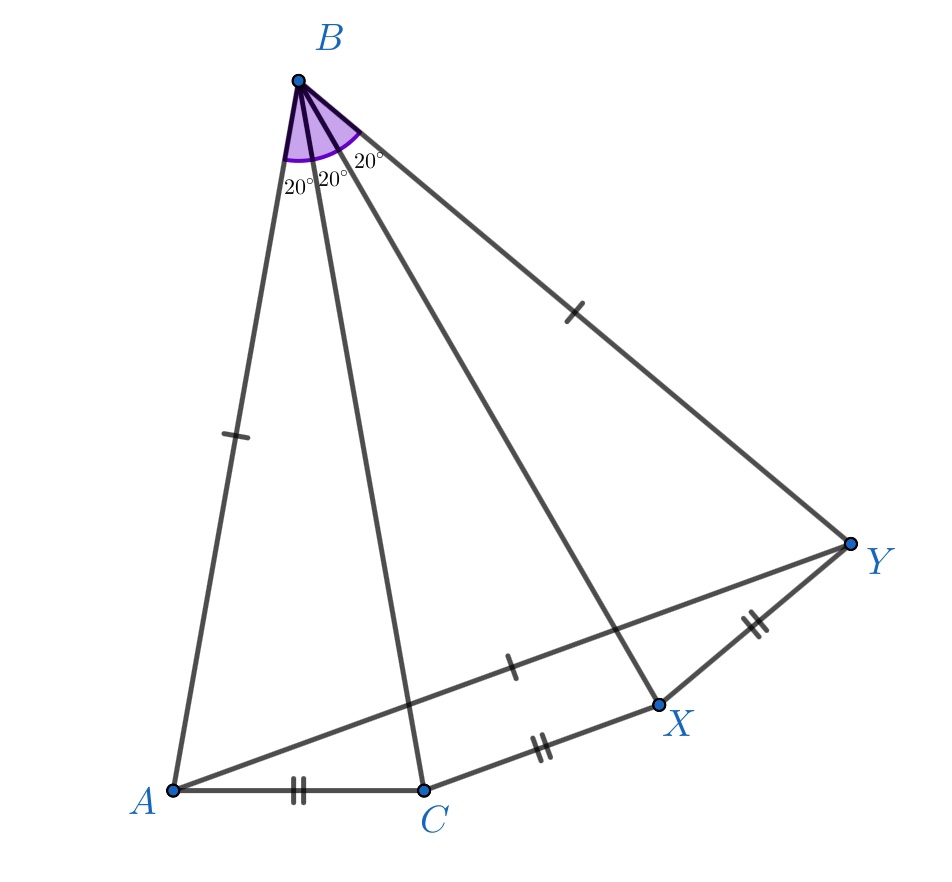
Заметим, что — равносторонний. Запишем неравенство для ломаной
:
Ошибка.
Попробуйте повторить позже
Вершины четырехугольника
лежат соответственно на сторонах
квадрата
Найти
наименьший возможный периметр четырехугольника
если
см,
см и
Источники:
Подсказка 1
Очень часто, когда просят найти наименьший периметр, помогает сводить задачу к неравенству ломаной. Т.е. все нужные нам отрезки "сложить" в одну ломаную. Каким образом это удобнее всего сделать в нашем случае, учитывая, что у нас квадрат?
Подсказка 2
Квадрат удобно отражать и переносить. Осталось лишь подумать, относительно каких сторон это делать, чтобы каждый раз у нас появлялся новый кусочек ломаной, которую хотим создать из нужных отрезков.
Первое решение.
.png)
(везде ниже единицы измерения — сантиметры)
Из первого условия Сведём задачу к неравенству ломаной. Для этого отразим квадрат относительно
(
а затем относительно
(
Легко видеть, что
Далее отразим
относительно
в точку
Можно считать, что точку
мы ранее также отражали относительно
потому
По неравенству ломаной
Отрезок
фиксирован, потому достаточно
посчитать длину
(нетрудно видеть, что минимум достигается подбором точек
и
Используем теорему Пифагора
(“проекция на
”) и
откуда
Второе решение.
Введём систему координат с центром в точке ось
направим вдоль
ось
вдоль
возьмём за единицу измерения
см. Обозначим координату точки
по оси
за
координату точки
по оси
— за
Тогда по теореме Пифагора периметр
четырёхугольника
равен
Отметим точки с соответствующими им координатами: По неравенству ломаной
причём равенство достигается при
Итак, минимальный периметр равен
см
Ошибка.
Попробуйте повторить позже
Длины сторон многоугольника равны Квадратный трехчлен
таков, что
Докажите, что если
— сумма длин нескольких сторон многоугольника,
— сумма длин остальных его сторон, то
Источники:
Подсказка 1
В данной задаче мы хотим доказать, что квадратный трехчлен обладает некоторой симметрией. Какой симметрий обладает парабола?
Подсказка 2
График квадратного трехчлена обладает осевой симметрией: f(x) = f(a - x) для некоторого фиксированного a. Как эта симметрия применима к нашей задаче?
Подсказка 3
Пусть S - сумма всех сторон многоугольника. Тогда нам дано, что f(a_1) = f(S - a_1).
Попробуйте подставить эти выражения в квадратный трехчлен в общем виде, и из частного случая симметрии найти общий случай симметрии.
Первое решение.
Из графика квадратного трехчлена видим, что либо
и
расположены на числовой оси симметрично
относительно точки
— абсциссы вершины параболы, т.е при
Но для многоугольника
поэтому
Тогда
значит,
______________________________________________________________________________________________________________________________________________________
Второе решение.
Переформулируем задачу в непрерывном виде , тогда нашлось такое
(
, что
, то есть
Может ли быть так, что ? Нет, поскольку в многоугольнике хотя бы 3 стороны и выполнено неравенство ломаной — если вычесть
из обеих частей
, то остальные стороны будут образовывать ломаную, соединяющую начало и конец стороны, что соответствует длине
.
Но тогда
, далее
, но подставляя это аналогично (*), получим
, что
выполнено из
, что и требовалось.


