Антипараллельность
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник 
; 
, 
, 
— его высоты, 
— центр описанной окружности. Докажите, что касательная в
точке 
к описанной окружности параллельна прямой 
, а 
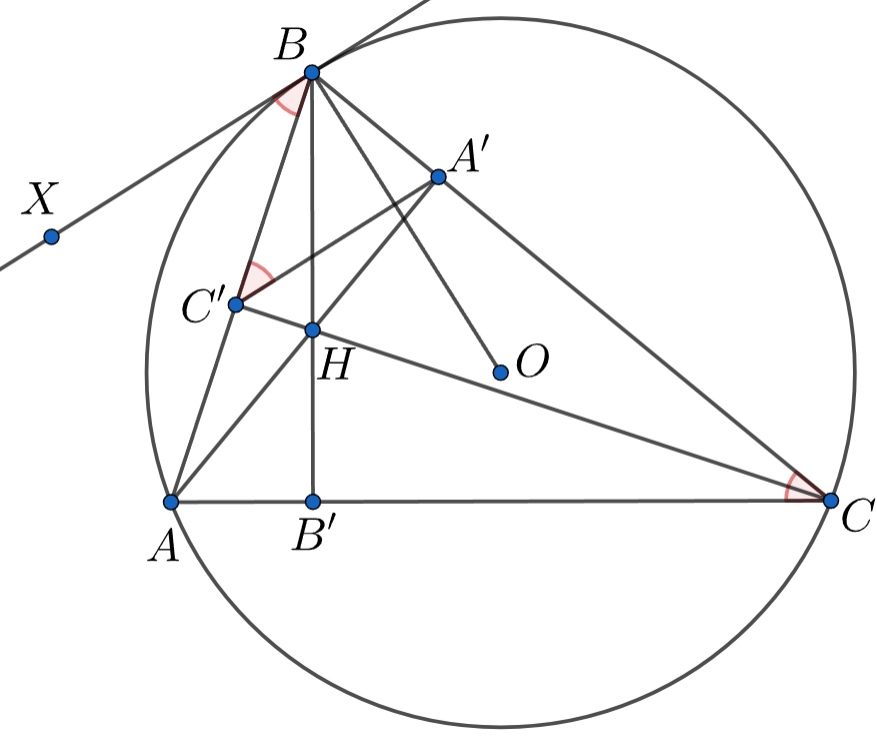
В силу антипараллельности 
и 
имеем 
Также 
как угол между хордой и касательной. Теперь
видно, что 
Понятно, что достаточно доказать перпендикулярность 
и 
Это так, потому что 
является радиусом проведенным к точке
касания прямой 
с окружностью.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
