Антипараллельность

Первое решение.

Четырехугольник вписанный, поэтому прямые и антипараллельны относительно угла, образованного прямыми и но параллельна поэтому прямые и антипараллельны, т.е. четырехугольник вписан в окружность, следовательно,

а значит четырехугольник так же является вписанным, а прямые и антипараллельны. Последняя в свою очередь антипараллельна т.е. прямые и параллельны.

Таким образом, прямые и перпендикулярны, поскольку перпендикулярны прямые им параллельные — и

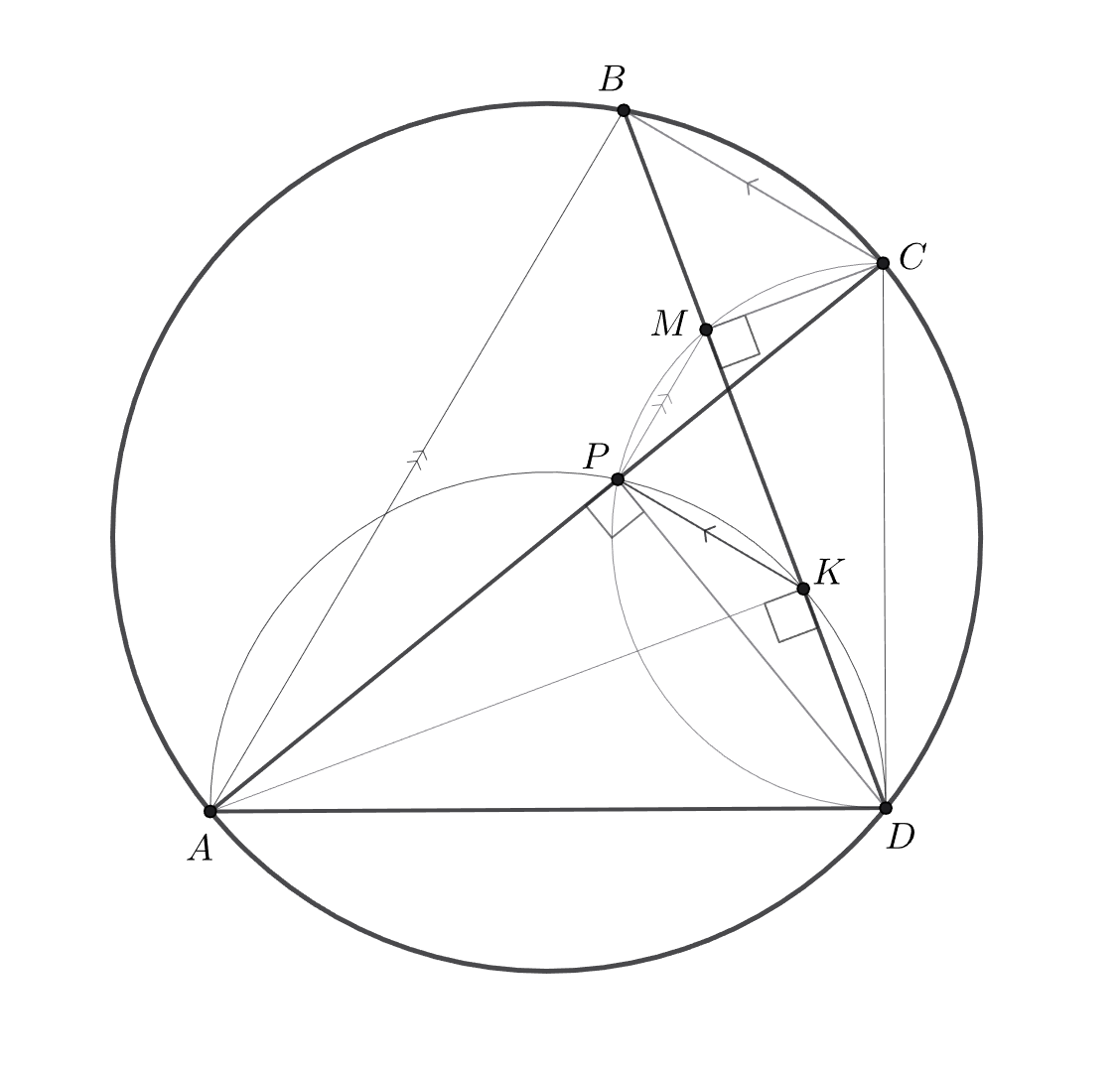
Второе решение.

Пусть диагонали четырёхугольника пересекаются в точке а точка расположена между и Тогда

значит, из точек и лежащих по одну сторону от прямой отрезок виден под одним и тем же углом, поэтому точки и лежат на одной окружности, а т.к. то — диаметр этой окружности, значит, Из точек и отрезок виден под прямым углом, значит, эти точки лежат на окружности с диаметром Тогда

поэтому а т.к. и то что и требовалось доказать. Аналогично для случая, когда точка расположена между и

_________________________________________________________________________________________________________________________________________________________________________________

Третье решение.

Обозначим через точку пересечения диагоналей и Пусть для определенности точка лежит на отрезке

Пусть прямая, проходящая через параллельно пересекает в точке Треугольник и подобны (так как их стороны параллельны), откуда Прямоугольные треугольники и также подобны, поэтому Перемножая полученные равенства, получаем Но по теореме Фалеса Следовательно,

откуда Значит, и