Лемма о трезубце
Ошибка.
Попробуйте повторить позже
Точка — центр вписанной окружности треугольника
— середина стороны
а
— середина дуги
описанной окружности, не содержащей
Оказалось, что
В каком отношении точка
делит отрезок
Источники:
Подсказка 1
Такс, давайте подумаем, а что это вообще за точка W? Как её можно использовать?
Подсказка 2
Да, поскольку точка W — середина дуги AB, то она лежит на биссектрисе угла C! А теперь, вспомним один факт: внутренняя и внешняя биссектриса одного и того же угла перпендикулярны. А также мы знаем, что ∠AIM — прямой! Какое дополнительное построение теперь хочется сделать?
Подсказка 3
Да, хочется построить внешнюю биссектрису ∠A. Теперь, давайте отметим все углы и увидим параллельность двух прямых на рисунке! Что теперь можно сказать про отрезок IM?
Подсказка 4
Да, IM — средняя линия треугольника ACJ, где J — центр вневписанной окружности! А что можно сказать про точку W? Верно W — середина IJ!
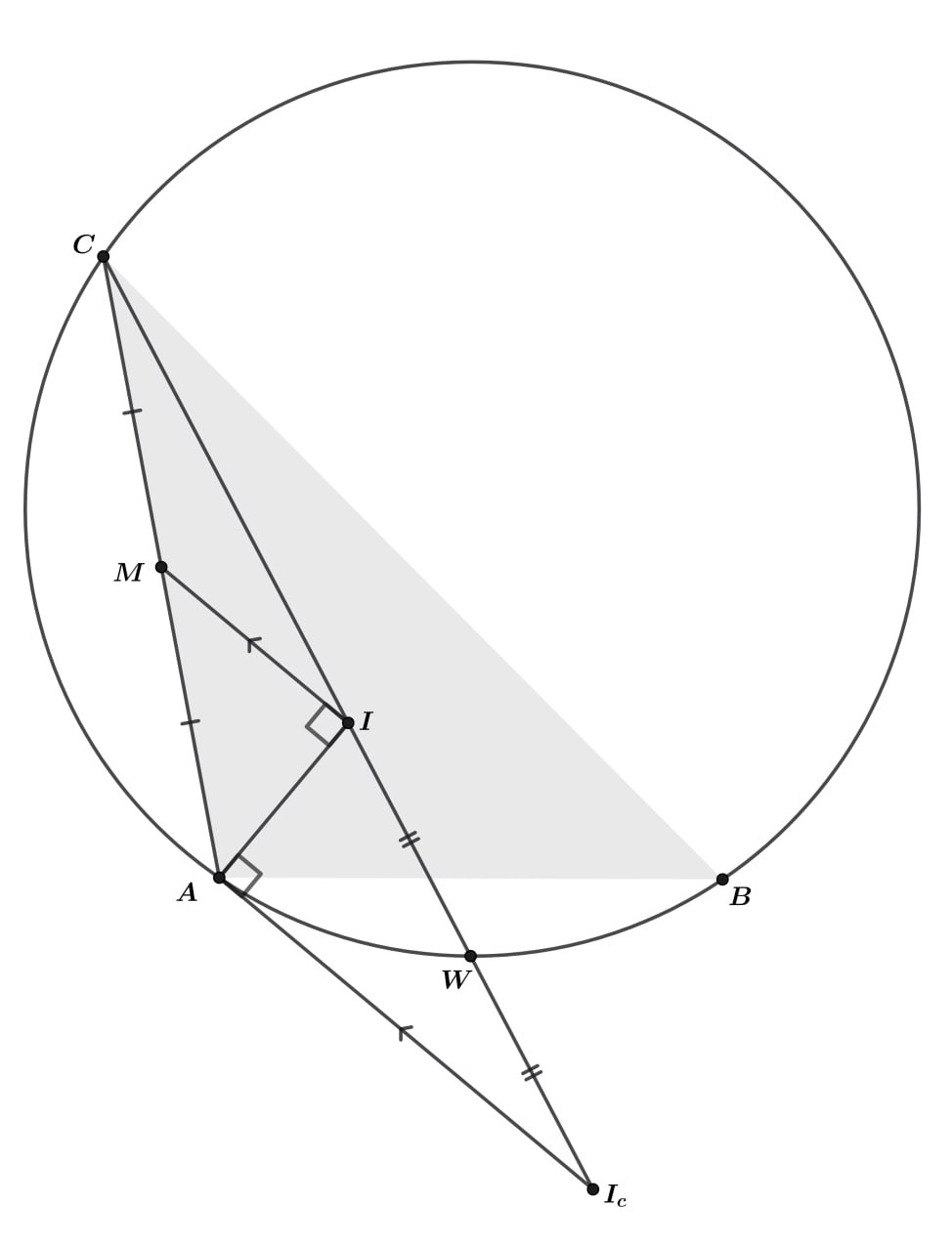
Давайте поймем, как реализовать странное условие про угол. Вспомним про то, что внутренняя и внешняя биссектрисы одно и того же угла
перпендикулярны. Тогда давайте дополнительно отметим центр вневписанной окружности данного треугольника, касающейся стороны
Пусть это
Значит,
Так как то
– средняя линия треугольника
По лемме о трезубце
– середина
следовательно,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




