Лемма о трезубце
Ошибка.
Попробуйте повторить позже
Около треугольника описана окружность. Хорды, соединяющие середину дуги
с серединами дуг
и
, пересекает
стороны
и
в точках
и
соответственно. Докажите, что точки
,
и центр вписанной в треугольник
окружности
лежат на одной прямой.
Источники:
Подсказка 1
Давайте вначале забудем про точку H и попробуем что-то доказать про точку K, а точнее, про отрезок KI.
Подсказка 2
Нам в задаче даны середины дуг и центр вписанной окружности, поэтому сразу хочется использовать...
Подсказка 3
Лемму о трезубце! Мы получаем много равных отрезков. И что тогда можно сказать доказать про треугольник AKI?
Подсказка 4
Он равнобедренный! А равнобедренность влечёт равенство уголков...
Подсказка 5
Простым счетом углов доказываем, что KI параллельно AC. А теперь нужно вспомнить про точку H и про то, что нам надо доказать, и понять, что задача на самом деле решена.
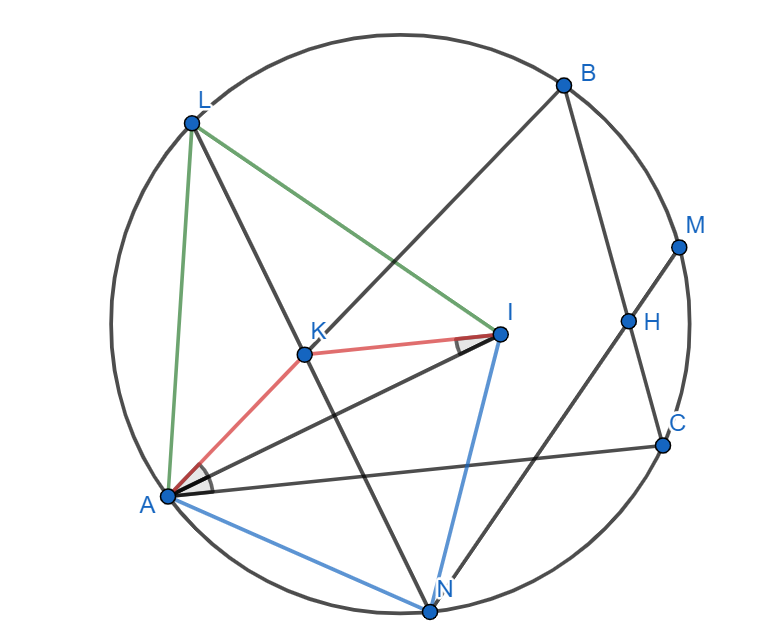
Обозначим за середины дуг за
соответсвенно, а также пусть
центр вписанной окружности треугольника
Тогда, по лемме о трезубце имеем:
Значит, — серединный перпендикуляр к отрезку
Отсюда следует, что
Теперь немного посчитаем углы. В силу
равенства
получим:
Вспомним, что
- биссектриса угла
Тогда
В итоге,
имеем:
Аналогично доказывается, что Но так как через одну точку, не лежащей на заданной прямой, можно провести только одну
прямую, параллельную данной, то точки
лежат на одной прямой.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




