Лемма о трезубце

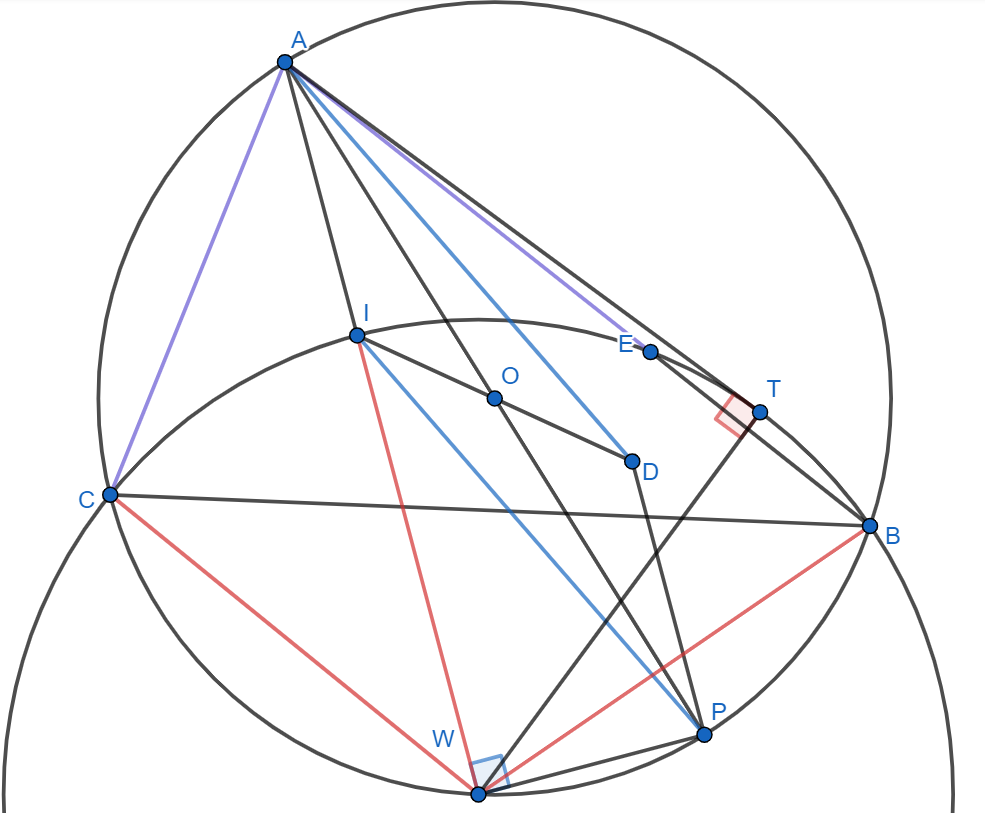
Пусть биссектриса пересекает описанную окружность в точке . Проведем диаметр . Тогда - параллелограмм и . Тогда доказываемое равенство можно записать в виде:

Кроме того, так как - диаметр окружности, то угол - прямой. Тогда правую часть равенства (1) можно преобразовать:

Таким образом, задача сводится к доказательству равенства

Воспользуемся известным фактом: , который называют теоремой трилистника или леммой о трезубце. Центр описанной окружности треугольника BIC лежит на биссектрисе угла , поэтому точки пересечения этой окружности со сторонами угла попарно симметричны относительно биссектрисы . В частности, симметричны точки и , значит, .

Пусть - касательная к описанной окружности треугольника ВIC. Тогда

Из треугольника по теореме Пифагора

Из равенств (3) и (4), учитывая также, что , получим:

то есть равенство (2), которое равносильно утверждению задачи.

В заключительной части решения можно обойтись без теоремы Пифагора, если использовать степень точки относительно окружности

Это утверждение, равно как и теорему о трилистнике, школьники могут использовать без доказательства.