Лемма о трезубце
Ошибка.
Попробуйте повторить позже
На дугах и
окружности, описанной около треугольника
выбраны соответственно точки
и
так, что прямые
и
параллельны. Докажите, что центры вписанных окружностей треугольников
и
равноудалены от середины дуги
Источники:
Подсказка 1.
Для начала надо кое-что понять про центры вписанных окружностей. Какое утверждение в этом поможет?
Подсказка 2.
Правильно, лемма о трезубце! Давайте отметим середины дуг AK и CL и обозначим их через P и Q соответственно. Теперь надо бы кое-что понять про точки P и Q. Для этого надо вспомнить, что KL ∥ AC.
Подсказка 3.
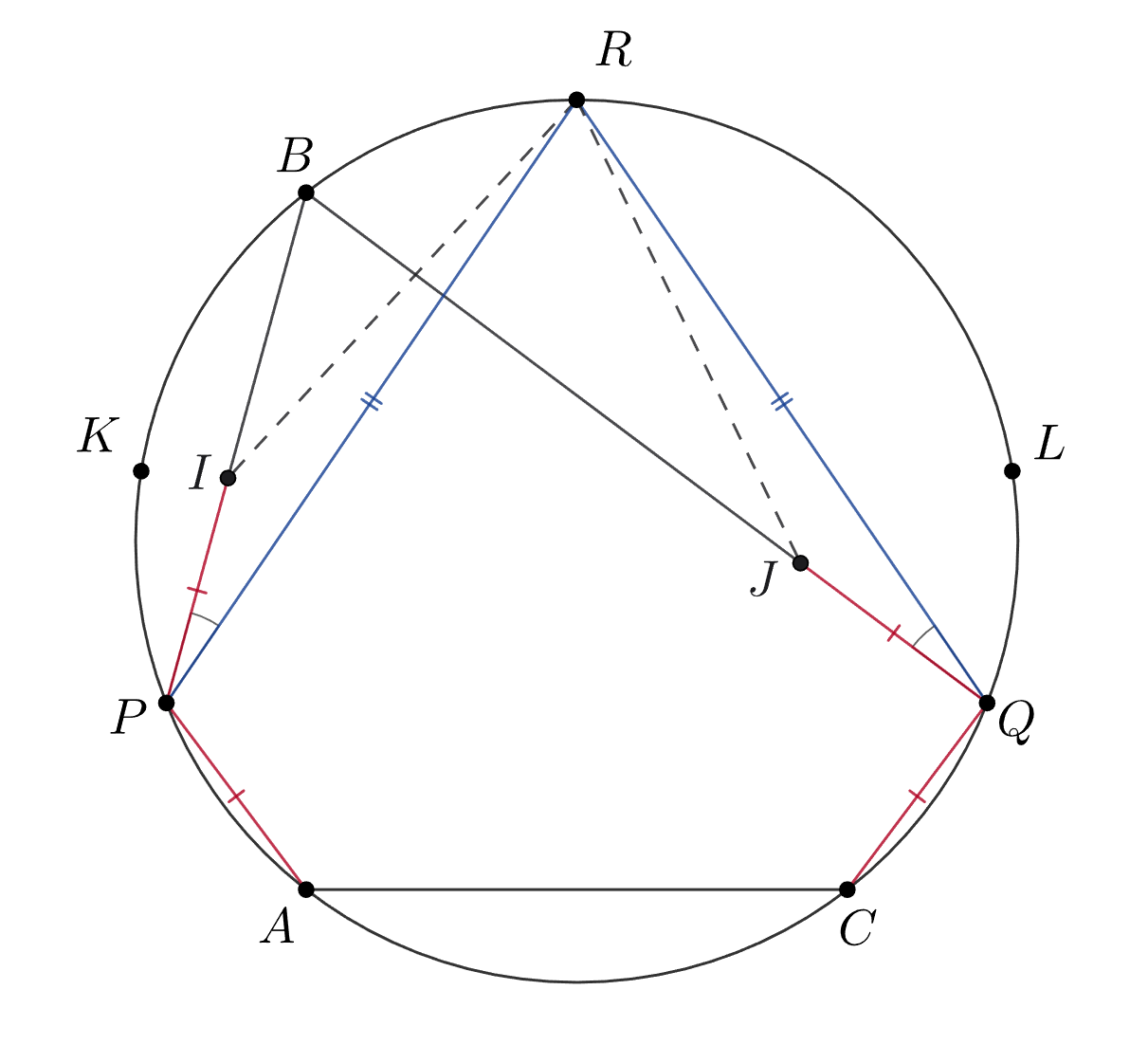
Пусть R — середина дуги ABC, а I и J — центры вписанных окружностей. Доказать равенство отрезков IR и RJ довольно проблематично. Но можно доказать равенство некоторых объектов, в которые они входят, из которого будет следовать их равенство.
Подсказка 4.
Попробуйте доказать равенство треугольников IRP и JRQ
Обозначим через — центры вписанных окружностей соответственно, через
— середины дуг
соответственно. Пары точек
и
и
симметричны относительно серединного перпендикуляра к стороне
следовательно,
По лемме о трезубце же
Наконец, углы и
равны, поскольку опираются на равные дуги, следовательно, равны треугольники
и
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




