Лемма о трезубце
Ошибка.
Попробуйте повторить позже
[Внешняя лемма о трезубце.] Докажите, что середина дуги описанной окружности треугольника
равноудалена от точек
и двух центров вневписанных окружностей, касающихся сторон
и
Подсказка 1
Будет удобно, если указанные в условии точки лежат на одной прямой. Тогда мы сможем работать с четырёхугольником, образованным центрами вневписанных окружностей и вершинами нашего треугольника.
Подсказка 2
Центры вневписанных окружностей и T (середина дуги BAC) лежат на внешней биссектрисе угла BAC! Отлично, теперь попробуем сделать какие-то выводы про образовавшийся большой четырёхугольник. Чем для треугольника ABC являются его диагонали? Что можно сказать про углы внутри него?
Подсказка 3
Диагонали четырёхугольника являются биссектрисами углов треугольника ABC! А чем для треугольника ABC являются его стороны?
Подсказка 4
Одна из пар сторон большого четырёхугольника является парой внешних биссектрис треугольника ABC! Что тогда можно сказать про связь его диагоналей и сторон?
Подсказка 5
Диагонали перпендикулярны одной из пар противоположных сторон! Получается, внутри четырёхугольника есть два угла по 90°. Какие выводы можно сделать о такой фигуре?
Подсказка 6
Четырёхугольник вписан! Осталось лишь аккуратно показать, почему его T — середина его стороны ;)
Пусть — центры вневписанных окружностей, которые касаются сторон
и
соответственно. Биссектриса
внешнего угла
перпендикулярна биссектрисе
внутреннего угла, т.е.
Аналогично,
значит, точки
лежат
на одной окружности.
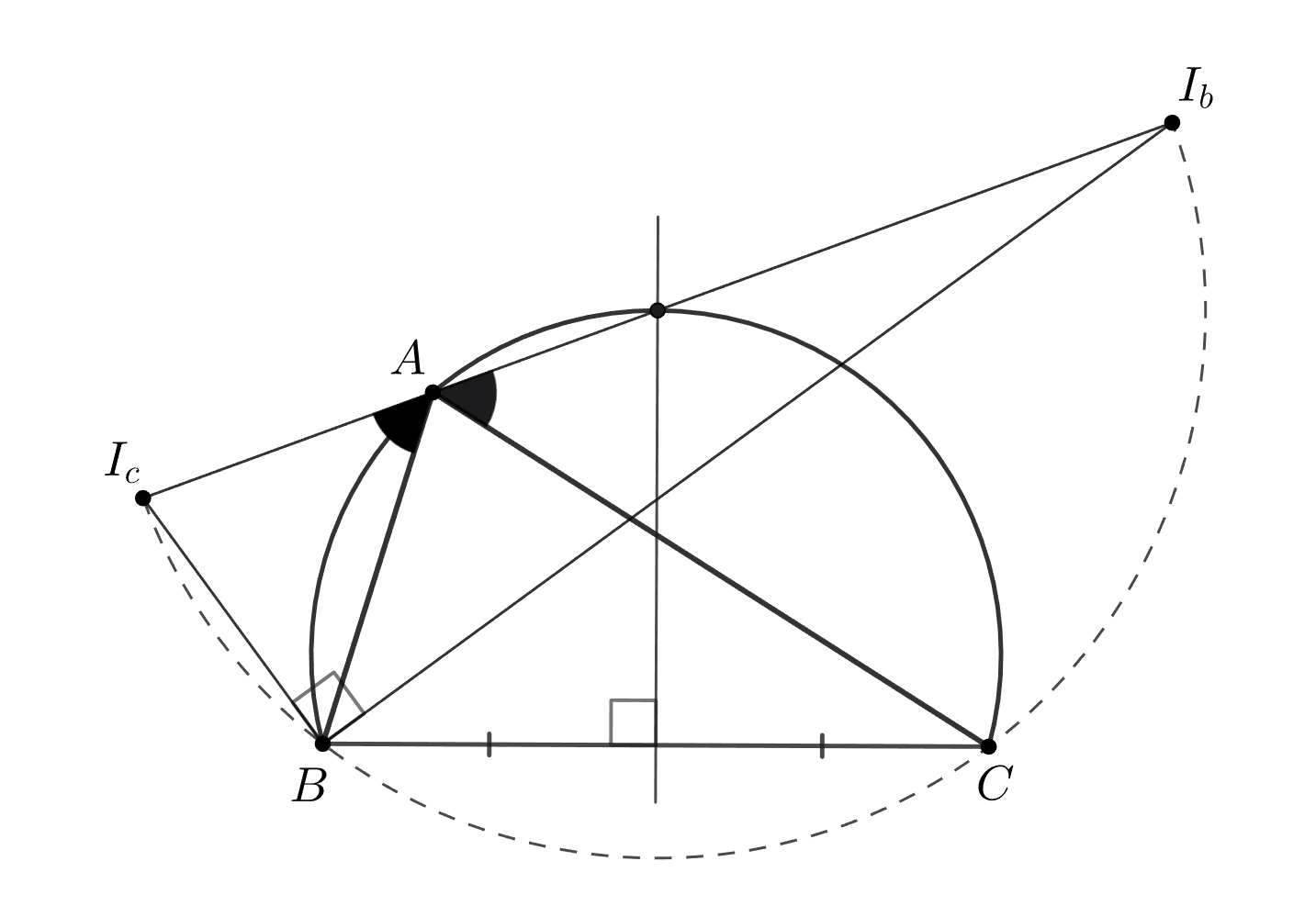
Осталось заметить, что центр окружности лежит на диаметре и на серединном перпендикуляре к стороне
но такая точка
единственна и середина дуги
удовлетворяет этим условиям.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




