Использование средней линии и середин отрезков через векторы
Ошибка.
Попробуйте повторить позже
Центроидом четырехугольника будем называть точку пересечения двух прямых, соединяющих середины его противоположных сторон.
Шестиугольник вписан в окружность
с центром
Известно, что
и
Пусть
и
—
центроиды четырехугольников
и
соответственно. Докажите, что высоты треугольника
пересекаются в точке
Источники:
Подсказка 1
Сначала хочется разобраться с равенствами сторон. Заметим, что в силу этих равенств три четырёхугольника из условия являются равнобедренными трапециями! Тогда у них равны диагонали. Что тогда можно сказать про связь этих диагоналей с центром O?
Подсказка 2
Правильно, они равноудалены от O. Тогда их середины P, Q, R равноудалены от O, т.е. O является центром описанной окружности △PQR. Почему это хорошее наблюдение? Ну, кажется, что центроиды как-то связаны со сторонами △PQR.
Подсказка 3
Действительно, из симметрии трапеций центроиды вроде бы должны быть серединами соответствующих сторон △PQR. На самом деле это правда, попробуйте доказать это утверждение в таком виде: середины сторон △PQR являются центроидами соответствующих трапеций. Этот факт верен и для произвольного четырёхугольника, попробуйте его также доказать, это довольно важная лемма. Теперь, когда мы доказали эту крутую лемму, поймём, как связаны △PQR и △XYZ.
Подсказка 4
Стороны △XYZ являются средними линиями △PQR, т.е. параллельны его сторонам. Постойте, но теперь утверждение задачи очевидно! Ведь т.к. O является центром описанной окружности △PQR, то мы можем провести серединные перпендикуляры. А ведь для △XYZ они являются... :)
Важная лемма о центроиде. Центроид четырехугольника является серединой отрезка, соединяющего середины его диагоналей.
Первый способ доказательства. Пусть — данный четырехугольник, а
— середина отрезка
(для всех пар
индексов). Тогда
— средняя линия треугольника
поэтому
Аналогично
поэтому
Таким же образом доказывается параллельность
и
Значит,
— параллелограмм,
тем самым середина отрезка
лежит на прямой
Аналогично, середина
лежит на прямой
таким
образом, эта середина является центроидом. Утверждение доказано.
Второй способ доказательства. Пусть у четырёхугольника точки
— середины
. Пусть
— середины
Для центроида
выполнено
поскольку
— параллелограмм. Заметим, что
а
также
откуда
Тогда уже для
— середины
получаем
Отсюда Утверждение доказано.
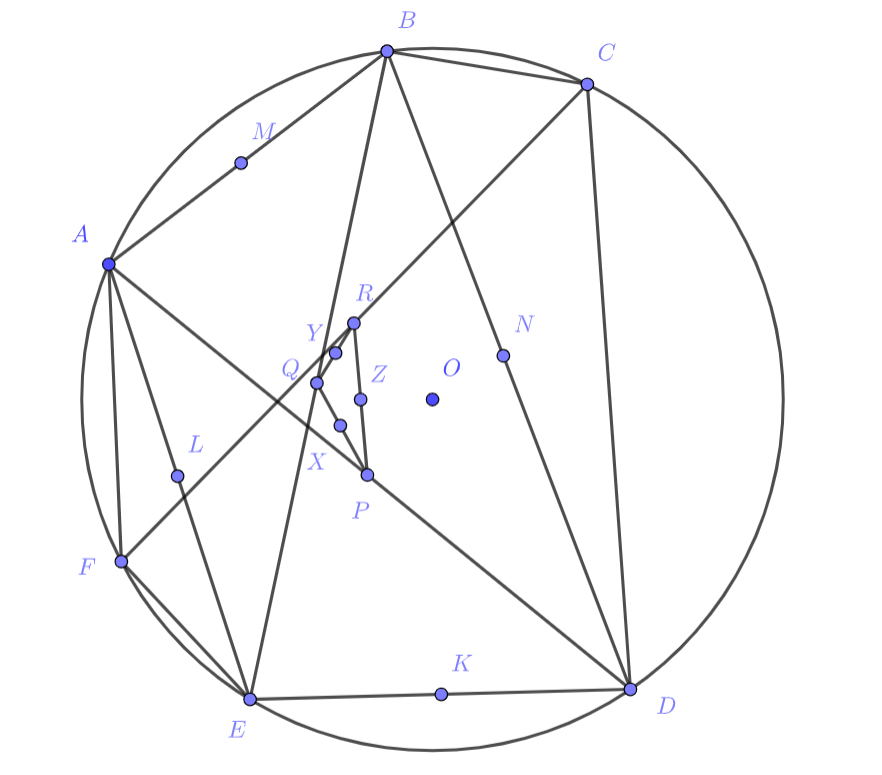
Решение. Проведем диагонали пусть
соответственно — их середины. По Важной лемме о центроиде середины
отрезков
и есть центроиды четырехугольников
Итак,
— соответственно середины отрезков
Из равенства отрезков и
следует равенство дуг, откуда
отсюда
и
равноудалены от
Тогда
— серединный перпендикуляр к
Так как
как средняя линия, то
Аналогично
значит,
— ортоцентр треугольника
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




