Базовые операции с векторами на плоскости
Ошибка.
Попробуйте повторить позже
Упростите выражение
Вспомним, что для любых точек верно
а также, что сложение векторов коммутативно и ассоциативно, то есть
и
Исходя из этих свойств:
Ошибка.
Попробуйте повторить позже
Упростите выражение
Ошибка.
Попробуйте повторить позже
Ошибка.
Попробуйте повторить позже
В четырёхугольнике точка
— середина
— середина
Докажите, что
Когда достигается равенство?
Представим вектор в следующем виде:
Так как вектора и
и
равны по модулю и противоположно направленны, то
Тогда по неравенству треугольника получим, что
Равенство достигается, когда сонаправлен
то есть, когда
Когда
Ошибка.
Попробуйте повторить позже
Пусть и
— два параллелограмма с общей вершиной. Докажите, что один из векторов
и
коллинеарен
сумме двух других.
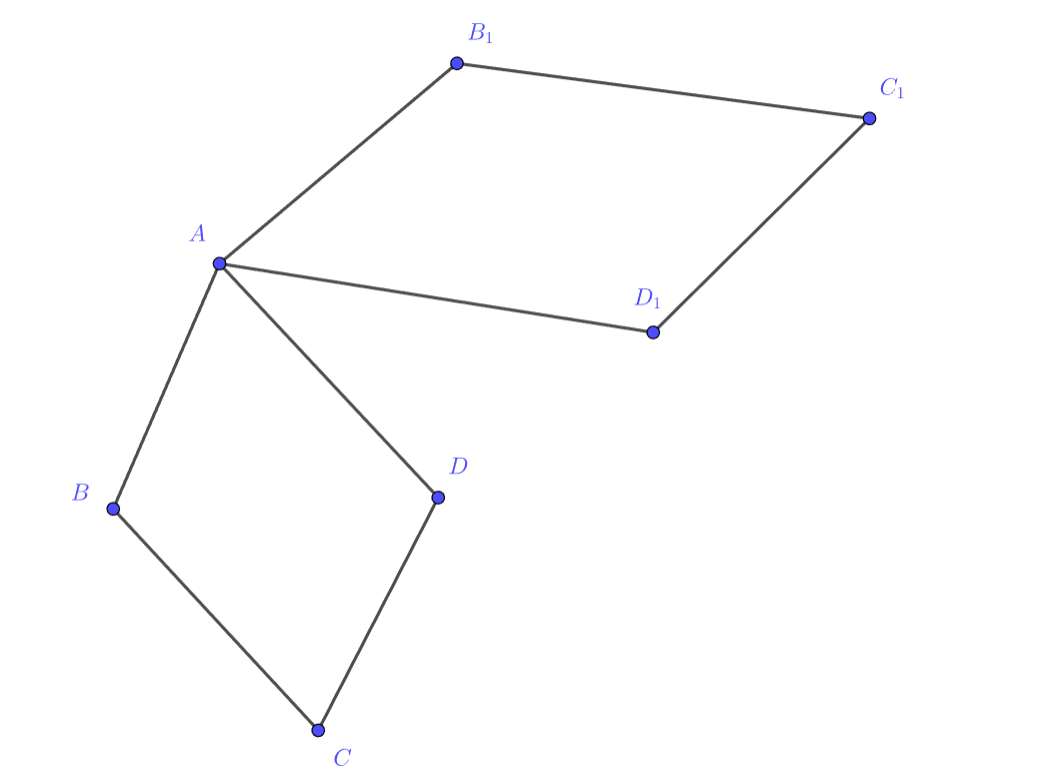
Выразим каждый из этих векторов через
Наконец,
Ошибка.
Попробуйте повторить позже
В треугольнике на стороне
выбраны точки
и
так, что
а на стороне
— точки
и
так, что
Докажите, что
Рассмотрим для определенности конфигурацию, изображенную на рисунке
![]()
Тогда имеем следующие равенства:
Поскольку а
то сложив второе и третье равенства получим
Следовательно
Заметим, что при таком решении не существенно, как расположены точки и
Ошибка.
Попробуйте повторить позже
Дан четырёхугольник и
— середины сторон
и
соответственно. Известно, что
и
Докажите, что
— параллелограмм.
![]()
Так как точки и
являются серединами соответствующих сторон, то
Складывая, получим, что
Значит, данные отрезки можно параллельно перенести так, чтобы образовался четырёхугольник. Поскольку а
то полученный четырёхугольник является параллелограммом. Следовательно, прямые
и
параллельны и четырёхугольник
— параллелограмм, откуда следует, что отрезки
и
параллельны и равны. Но тогда стороны
и
параллельны и
равны, то есть
— параллелограмм.
Ошибка.
Попробуйте повторить позже
В трапеции c основаниями
и
оказалось, что
. В каком отношении диагональ
делит
диагональ
?
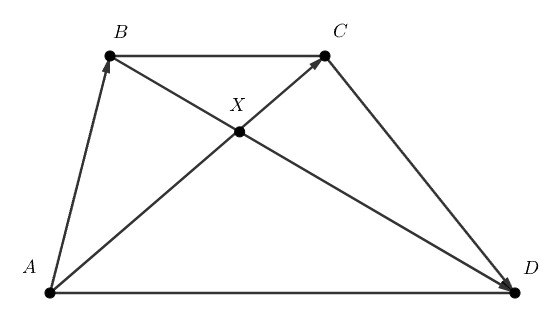
Распишем левую часть уравнения:
Подставляя последнее выражение в уравнение, получаем:
Распишем
Подставляя в уравнение получаем, что:
Из подобия треугольников, получаем, что искомое отношение
Ошибка.
Попробуйте повторить позже
Докажите, что сумма векторов, ведущих из центра правильного -угольника в его вершины, равна
.
Пусть мы имеем дело с -угольником. То есть, мы хотим понять, чему равна сумма
векторов, идущих из центра этого
-угольника к его вершинам. Обозначим
результат этой суммы за
Т.е. пускай
Сделаем такой трюк: повернём наш -угольник на
вокруг его центра. С одной стороны, раз мы
повернули картинку, то и результирующий вектор
должен повернуться на
С другой
стороны, понятно, что сумма
от поворота не изменилась, ведь наш
-угольник
как раз симметричен относительно такого поворота, т.е. при повороте на
он перешёл сам в
себя.
Следовательно, вектор который является результирующим вектором суммы
с
одной стороны не изменился, а с другой - повернулся на
Но вектор, который не меняется при
повороте на любой ненулевой угол, может быть только
Значит, тем самым, ничего не остаётся,
кроме как того, что
Что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
На окружности радиуса с центром
дано
точек
, лежащих по одну сторону от некоторого диаметра. Докажите,
что
.
Опустим везде обозначения векторов, поскольку больше ничего использовать не будем.
Будем доказывать по индукции. Не умаляя общности, можно считать, что векторы для каждого
отсортированы по
возрастанию тангенса угла наклона (или по часовой стрелке).
База индукции для (всего один вектор) очевидна,
пусть предположение верно для и для векторов
, то есть для
выполнено
.
Заметим, что каждый вектор из суммы лежит между
и
, тогда и
лежит между ними (если это не так, то хотя бы один
вектор в сумме имеет больший или меньший коэффициент наклона, чем у крайних, что невозможно). Далее пусть
,
тогда
— ромб и
— его диагональ и биссектриса
. Сам угол
меньше
по условию, тогда его
биссектриса образует острый угол с внутренним лучом
, то есть
. Пусть
(снова как векторы), то есть
, тогда
, как дополнение к острому и
(лежит напротив тупого угла). Шаг
индукции доказан.
Замечание. Если точки могут лежать на диаметре, то угол может достигать , откуда сторона в треугольнике останется
наибольшей, но теперь
может иметь нулевую длину и сумма останется на окружности при шаге индукции.
Ошибка.
Попробуйте повторить позже
Точка – центр квадрата
. Найдите какие-нибудь семь попарно неравных векторов с концами и началами в точках
,
сумма которых равна нулевому вектору.
Источники:
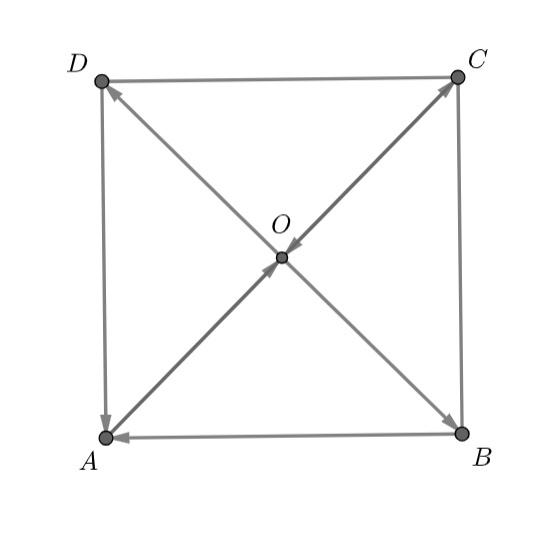
Например,


