Ортоцентр и его свойства

Обозначим через и точки пересечения медиан и высот треугольника а также отметим точку так, что

Пусть сфера построена на отрезке как на диаметре. Поскольку прямая перпендикулярна плоскости то точка лежит на Покажем, что на сфере лежит точка пересечения высот треугольника рассуждение для двух других треугольников аналогично.

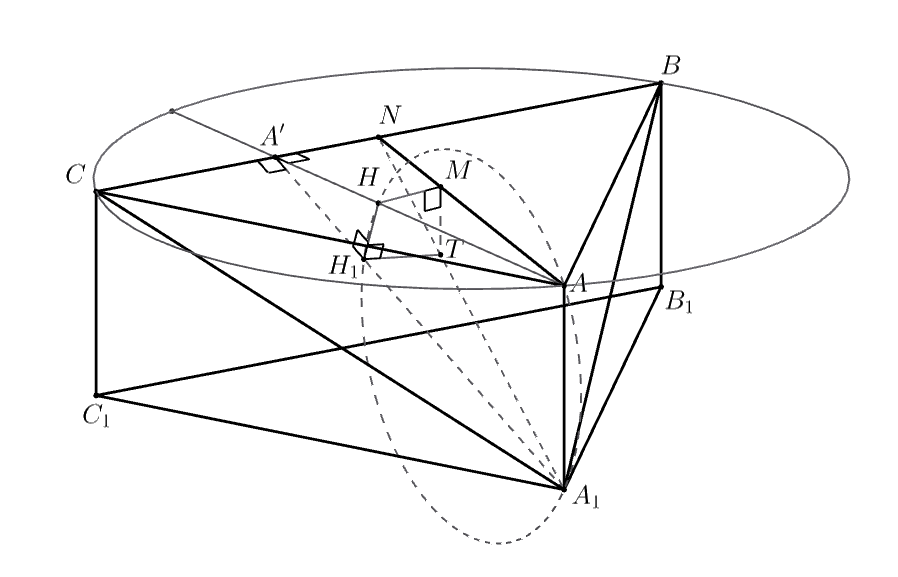
Обозначим через середину отрезка Поскольку точка лежит на отрезке в частности, она лежит в плоскости Пусть — высота треугольника Поскольку прямая перпендикулярна плоскости то а также по теореме о трёх перпендикулярах, то есть точка лежит на отрезке Поскольку точка, симметричная точке пересечения высот треугольника относительно прямой лежит на его описанной окружности, то Применяя то же рассуждение для треугольника мы получаем, что

Следовательно, четырёхугольник вписанный, поэтому Поскольку ещё и вновь применяя теорему о трёх перпендикулярах, мы получаем, что прямая перпендикулярна плоскости Значит, то есть точка лежит на сфере что и требовалось.

Аналогично доказывается, что точки пересечения высот треугольников и также лежат на сфере Таким образом, все пять точек (точки пересечения высот четырёх треугольников и точка пересечения медиан треугольника ) лежат на сфере