Ортоцентр и его свойства
Ошибка.
Попробуйте повторить позже
Точки и
симметричны центру
описанной около остроугольного треугольника
окружности относительно его сторон.
Докажите, что центром описанной окружности треугольника
является ортоцентр треугольника
Подсказка 1
Когда мы симметрично отражаем центр окружности, описанной вокруг треугольника, мы опускаем перпендикуляр из этой точки и удваиваем его, получая образ точки О. Пусть середины сторон AB и BC - это Х и Y. Что тогда можно сказать про отрезки XY и A₁C₁?
Подсказка 2
Эти отрезки параллельны, в силу того, что XY-средняя линия. OC₁A₁. Стоп… Но ведь она же и средняя линия треугольника ABC! А значит XY параллельно AC, а значит АС параллельно A₁C₁. Теперь посмотрим на всю картинку целиком. Центр описанной окружности треугольника A₁B₁C₁ - это точка пересечения серединных перпендикуляров к его сторонам. А через какую точку на картинке проходит серединный перпендикуляр к отрезку A₁C₁?
Подсказка 3
Рассмотрим треугольник OC₁A₁. Серединный перпендикуляр к OA₁ - это BY, к OC₁ - BX(все в силу симметрии), значит сервер к A₁C₁ проходит через точку B. Значит, и серединный перпендикуляр к B₁C₁ проходит через точку A. Но при этом чем являются серединные перпендикуляры для треугольника ABC? Поймите это, и задача решится сама!
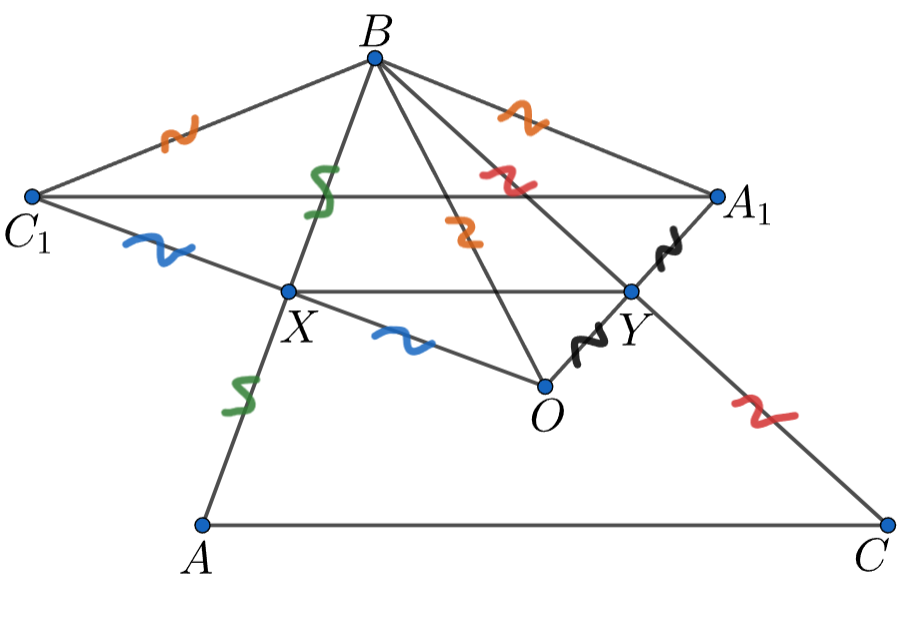
Пусть середины сторон
и
соответственно. Тогда
— средняя линия в
и
Отсюда следует, что
В силу симметрии
Таким образом,
— лежит на серединном перпендикуляре к
Из
параллельности
и
понимаем, что высота треугольника
из точки
— серединный перпендикуляр
Аналогично
другие высоты являются серединными перпендикулярами соответствующих сторон. Они пересекаются в ортоцентре, значит он является
искомым центром, что и требовалось.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




