Ортоцентр и его свойства
Ошибка.
Попробуйте повторить позже
В треугольнике точка
— центр описанной окружности, точка
— ортоцентр. Отрезки
и
параллельно перенесли и
последовательно приставили друг другу. Получилась ломаная. Докажите, что отрезок, соединяющий концы ломаной, равен и параллелен
Подсказка 1
Отрезки, которые друг от друга откладывают, и нам важно только расстояние между началом и концом… Да это же задача на векторы! То есть нас просят доказать векторное равенство OH=OA+OB+OC (всё в векторах). Сразу такое доказывать страшно и не понятно как. Может быть преобразовать два каких-то слагаемых из этой суммы, с помощью дополнительного построения?
Подсказка 2
Если у нас есть ортоцентр, то надо пользоваться его свойством. При этом таким свойством, чтобы где-то обнаружить отрезок BH, потому что в данный момент совершенно неясно, что с ним делать, а только с ним что-то делать и остается, так как оба отрезка: OH и OB, как-то с ним связаны. Так какое доп. построение здесь может зарешать?
Подсказка 3
Оп-па, можно отразить точку О относительно AC (пусть образ точки O- это О₁). Тогда OO₁=HB, по свойству ортоцентра, при этом, очевидно, HBOO₁ — параллелограмм. А значит, OH можно легко выразить через OB и OO₁. Осталось выразить, в силу того, что СOAO₁ — параллелограмм, сумму векторов OA+OC, после чего увидеть, что задача решена!
Иными словами, нас просят доказать векторное равенство
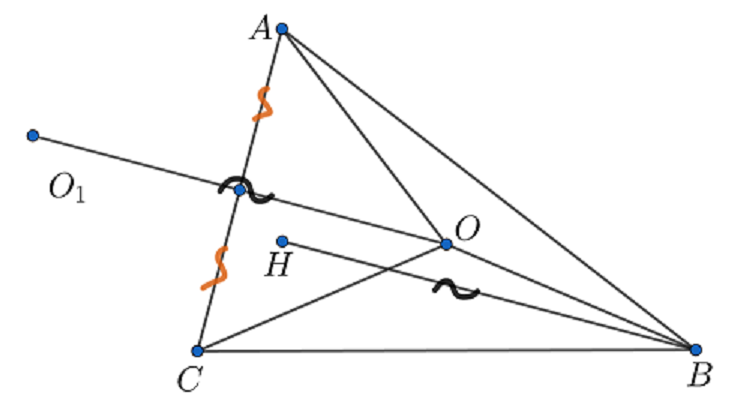
Пусть симметрична
относительно середины
тогда
По свойству ортоцентра и
значит
— параллелограмм, следовательно,
Таким образом,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




