Ортоцентр и его свойства
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведена высота
. Точки
и
- середины отрезков
и
. Докажите, что точка
пересечения перпендикуляров, опущенных из точек
и
на прямые
и
соответственно, равноудалена от точек
и
.
Источники:
Подсказка 1
Пусть перпендикуляры через M и N пересекаются в точке P. Тогда над каким дополнительным построением можно подумать, чтобы сделать MP и NP чем-то хорошим? Не забудьте, что M и N являются серединами отрезков.
Подсказка 2
Да, давайте попробуем опустить перпендикуляры X и Y из точки H на стороны треугольника. В таком случае MP и NP являются средними линиями, так как они параллельны основаниям и делят одну из сторон пополам. Но как тогда можно переформулировать вопрос задачи удобным образом для нас?
Подсказка 3
Верно, это значит, что четырёхугольник CXYB должен быть вписанным, так как в таком случае P центр описанной окружности и равноудален от B и C. Теперь только осталось посчитать уголочки, используя вписанный четырёхугольник и равные углы в прямоугольном треугольнике с проведённой высотой. Победа!
Первое решение.
Обозначим точку пересечения перпендикуляров, опущенных из точек и
на прямые
и
соответственно, через
,
а точки, симметричные
и
относительно прямых
и
, через
и
. Тогда прямые
и
—
cерединные перпендикуляры к отрезкам
и
, поэтому достаточно доказать, что четырёхугольник
—
вписанный.
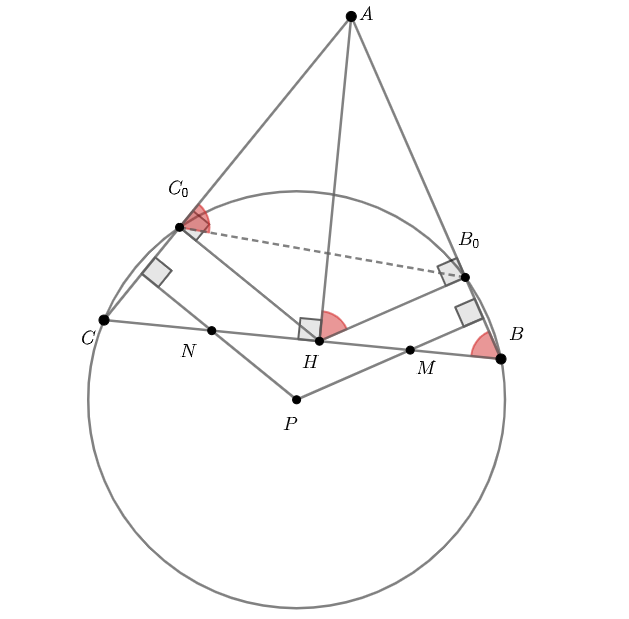
Заметим, что и
содержат средние линии треугольников
и
, параллельные сторонам
и
соответственно. Значит,
Четырёхугольник вписан в окружность, построенную на
как на диаметре, поэтому
по свойству
вписанных углов. При этом
. Значит, четырёхугольник
вписанный.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
Обозначим точку пересечения перпендикуляров, опущенных из точек и
на прямые
и
соответственно, через
, а точку
пересечения высот треугольника
— через
.
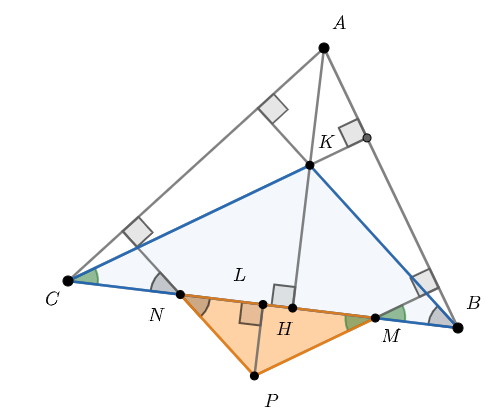
Тогда заметим, что треугольники и
подобны по двум углам. Действительно,
.
Аналогично, выполнено равенство
. Также заметим, что коэффициент подобия этих треугольников равен
, поскольку
.
Опустим из перпендикуляр
на
. Тогда из доказанного подобия следует, что
т. е.
. Следовательно,
а значит,
лежит на серединном перпендикуляре к отрезку
, откуда следует
требуемое.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




