Ортоцентр и его свойства
Ошибка.
Попробуйте повторить позже
Пусть и
— высоты остроугольного неравнобедренного треугольника
— середина
Окружность, описанная около
треугольника
пересекает прямую
в точке
Докажите, что
— касательная к описанной окружности треугольника
Подсказка 1
Для начала разберёмся, что нам вообще нужно доказать. Как можно понять, что прямая является касательной к окружности?
Подсказка 2
Мы знаем, что угол между хордой и касательной равен вписанному углу, опирающемуся на ту же дугу. Получается, нам нужно доказать равенство углов ABC и XAC. Попробуйте поотмечать на чертеже углы и поискать подобие.
Подсказка 3
Очень многое об углах могут сказать вписанные четырехугольники — а здесь их целых два! Каждый раз, когда мы видим в треугольнике 2 высоты, нужно вспоминать, что четырехугольник, диагоналями которого являются эти высоты, - вписанный. Поэтому какие четырехугольники в этой задаче будут вписанными?
Подсказка 4
Верно, это АВ₁А₁В и АМА₁Х. Что теперь мы можем сказать про треугольники АХВ₁ и А₁МВ?
Подсказка 5
Они подобны! Последнее, что нужно вспомнить, чтобы добить задачу - точка М является серединой АВ, а треугольник АВА₁ — прямоугольный. Чему тогда равен отрезок А₁М?
Т.к. то четырехугольник
вписанный. Значит,
Также, поскольку
четырехугольник
вписанный по условию,
Получаем, что
по двум
углам.
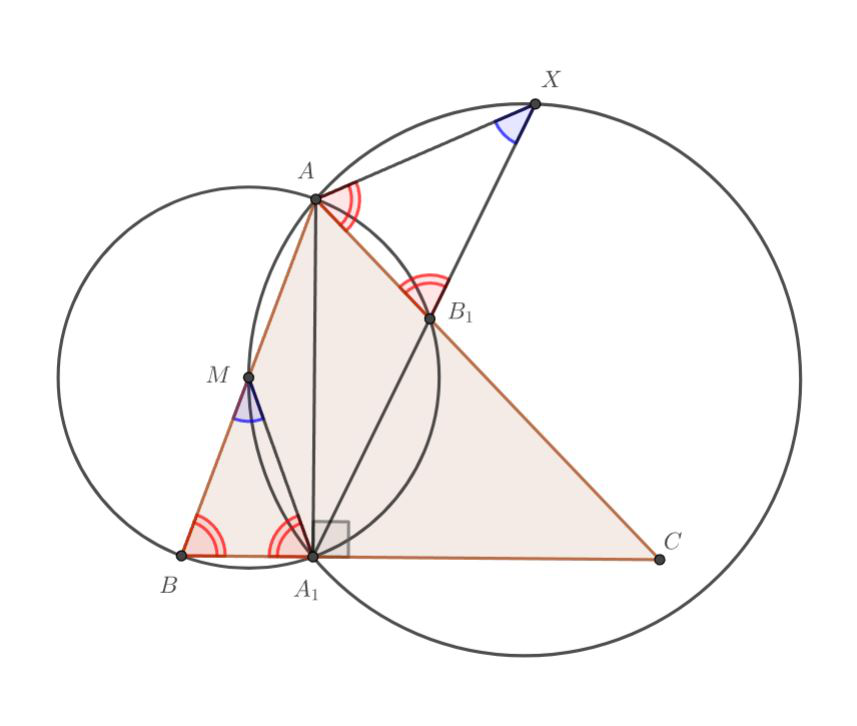
— середина гипотенузы
прямоугольного треугольника
Значит,
т.е. треугольник
равнобедренный. Но поскольку
то
Поскольку то
— касательная к описанной окружности треугольника
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




