Ортоцентр и его свойства
Ошибка.
Попробуйте повторить позже
Отрезок – диаметр описанной окружности остроугольного треугольника
. Через точку пересечения высот этого треугольника
провели прямую, параллельную стороне
, которая пересекает стороны
и
в точках
и
соответственно. Докажите, что
периметр треугольника
в два раза больше стороны
.
Подсказка 1
Просят доказать, что удвоенная сторона BC равна некоторому периметру. Мы знаем, что средняя линия равна половине стороны, которой она параллельна. Вот было бы здорово, если бы и отрезок BC был средней линией какого-нибудь треугольника!
Подсказка 2
У нас как раз есть уже параллельность BC и FE, осталось только продлить FE до пересечения с DB и DC (обозначим Х и Y), чтобы получить искомый треугольник. Самое время вспомнить, что Н лежит на FE. Какое свойство ортоцентра может помочь? Что можно сказать о том, в каком отношении ВС делит HD?
Подсказка 3
Чтобы завершить доказательство, обратите внимание на то, чем являются EB и FC в треугольниках XED и YFD соответственно.
Пусть и
— точки пересечения прямых
и
с прямой
.
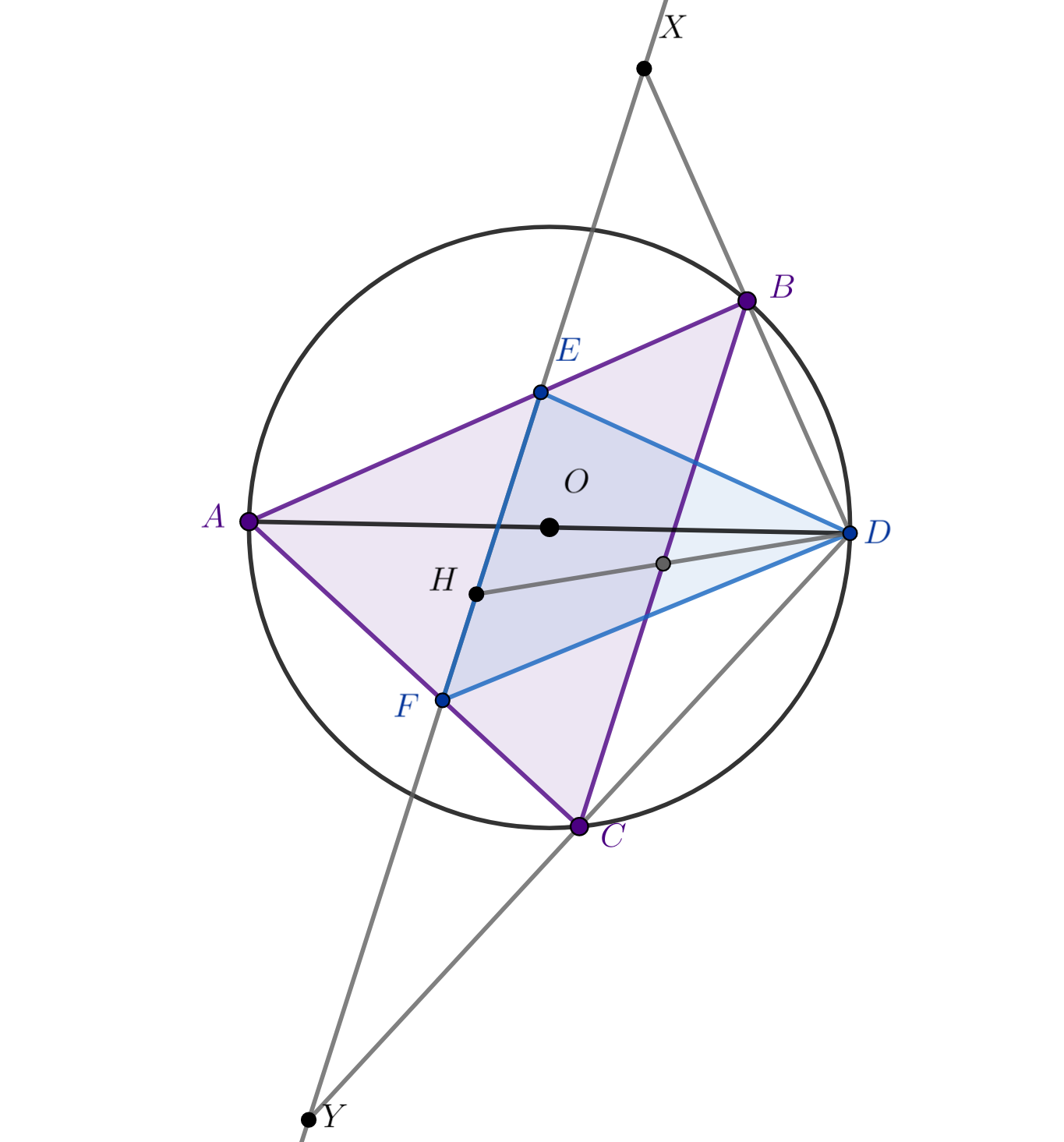
По свойству ортоцентра прямая делит отрезок
пополам, следовательно, так как прямые
и
параллельны, по
теореме Фалеса отрезки
и
делятся точками В и С пополам, значит,
— средняя линия в треугольника
.
Заметим, что угол
прямой, поэтому треугольник
равнобедренный, откуда
. Аналогично
,
следовательно,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




