Ортоцентр и его свойства
Ошибка.
Попробуйте повторить позже
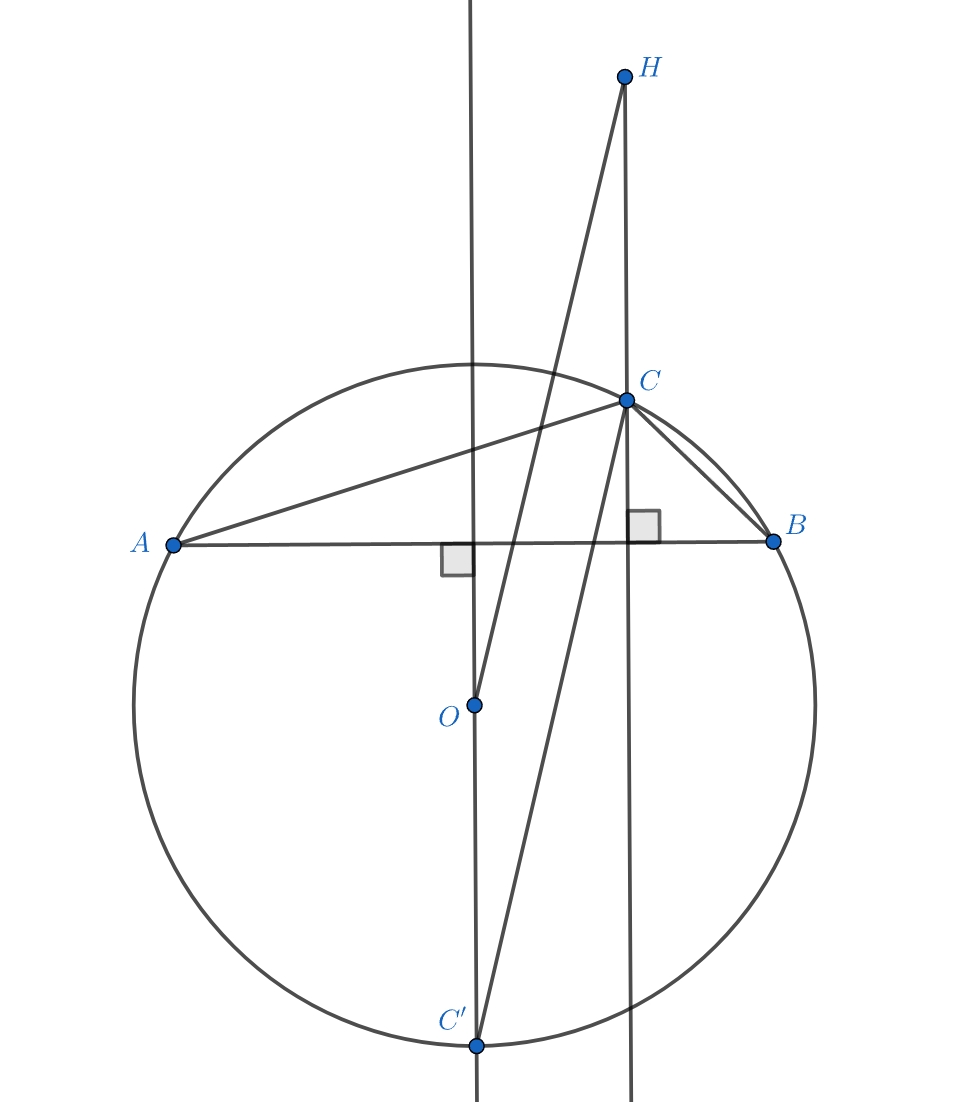
Прямая, соединяющая центр описанной окружности и точку пересечения высот неравнобедренного треугольника, параллельна биссектрисе одного из его углов. Чему равен этот угол?
Подсказка 1
Пусть биссектриса, упомянутая в условии, пересекает окружность в точке K. Что можно сказать о прямой ОК, где О — центр описанной окружности?
Подсказка 2
Конечно, она перпендикулярна одной из сторон треугольника! А ещё стороне всегда перпендикулярна высота, проведенная к ней. Так это же параллельность! А если ещё вспомнить про параллельность из условия, то можно получить какую-нибудь известную фигуру.
Подсказка 3
Две параллельности — это параллелограмм! Одна из его сторон — радиус. Попробуйте выразить противоположную сторону через радиус и угол, тогда, приравняв эти стороны, Вы сможете найти данный угол.
Пусть — центр описанной окружности треугольника
— его ортоцентр, и прямая
параллельна биссектрисе угла
Так как эта биссектриса пересекает описанную окружность в середине дуги
несодержащей
Следовательно,
четырехугольник
— параллелограмм и
С другой стороны, из свойств ортоцентра диаметры описанных окружностей около соответствующих подобных треугольников относятся с
коэффициентом подобия значит,
равен
или
Но в первом случае по свойству ортоцентра лучи и
симметричны относительно биссектрисы
так что прямая
не
может быть параллельна этой биссектрисе. Следовательно, подходит только
(в этом случае свойство ортоцентра про симметрию
тоже выполнено, но симметричны уже прямые, а не только лучи).
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




