Изогональное сопряжение

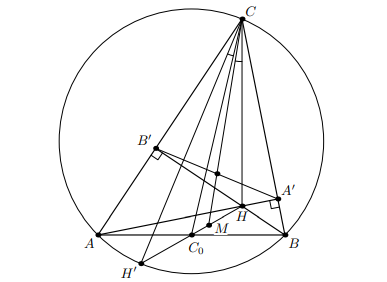
В такой конструкции сразу можно сказать, что антипараллельно относительно Поэтому если в условии дано, что прямая содержит медиану треугольника то эта прямая является симедианой в То есть мы поняли, что луч и луч являются изогоналями относительно если обозначить за середину стороны

По свойствам ортоцентра точка — отражение относительно — лежит на описанной окружности диаметрально противоположно При этом заметим, что

Лучи и являются ортоизогоналями угла (в треугольнике ортоцентр и центр описанной окружности изогонально сопряжены). Отсюда следует, что лучи и являются изогоналями также и для То есть — симедиана ещё и в Симедиана делит сторону в отношении квадратов прилежащих сторон, так что

Осталось заметить, что в данной конструкции и являются диаметрами в подобных и соответственно, так что их отношение равно коэффициенту подобия - косинусу угла

Итак,