01 Банк ФИПИ
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
На равномерно вращающемся диске жук переместился из точки А в точку В (см. рисунок). Как при этом изменились линейная скорость жука и частота его обращения вокруг оси O?
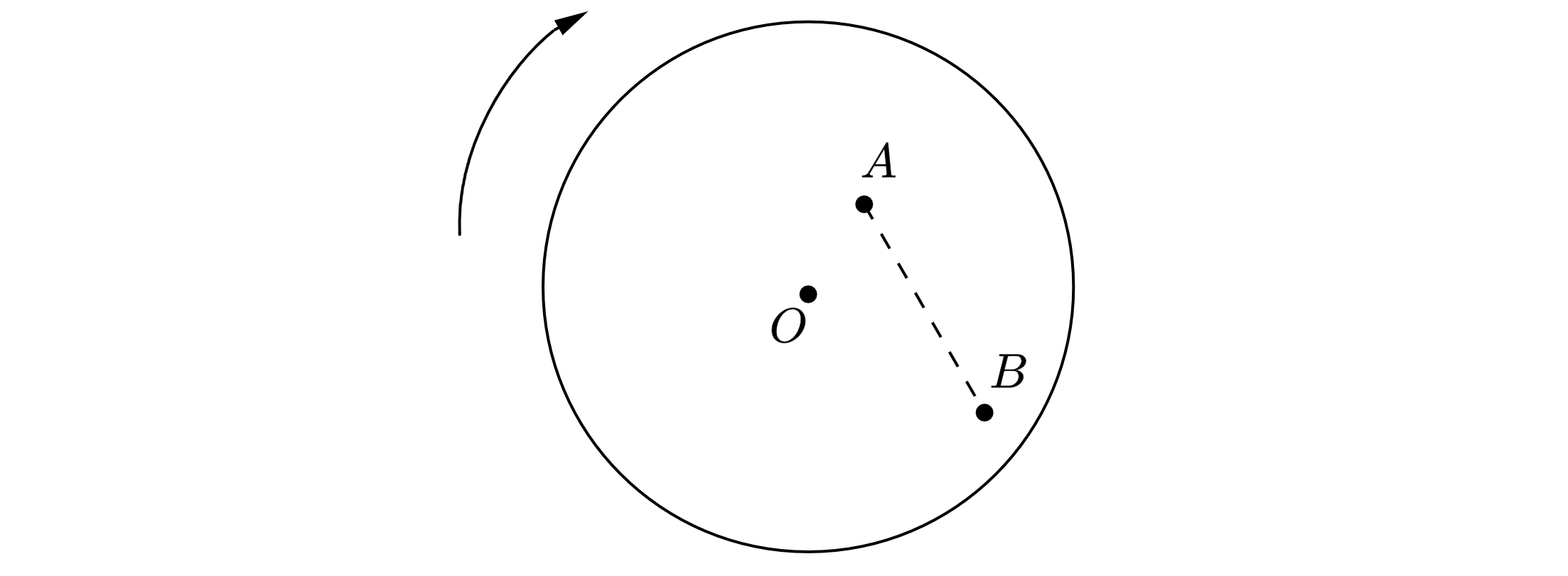
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Источники:
Угловая скорость диска постоянна для любых его точек. Линейная скорость
равна:
значит, при увеличении увеличивается и скорость.
Частота равна:
так как , то
Ошибка.
Попробуйте повторить позже
Муха сидела на равномерно вращающемся диске в точке А, а затем перелетела в точку В и села там (см. рисунок). Как в результате этого перемещения изменились линейная скорость мухи и частота её обращения на диске вокруг оси О?
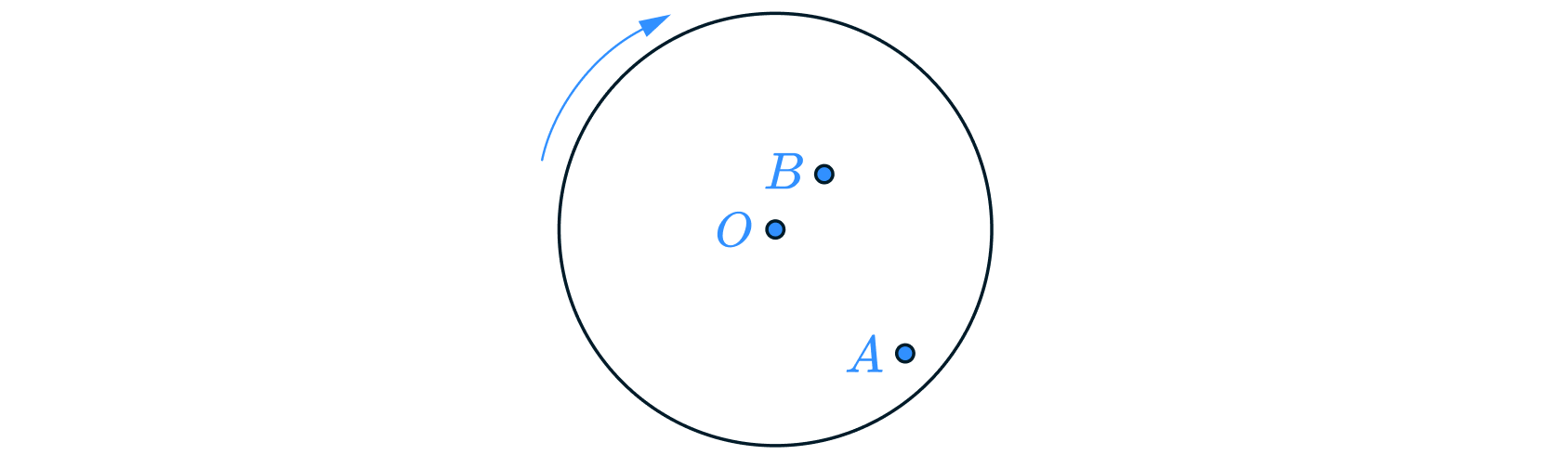
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Источники:
А) При перемещении из точки в точку
уменьшается радиус обращения мухи относительно точки
. Поскольку период
обращения диска не изменяется, то не изменяется и угловая скорость вращения диска. Формула для нахождения линейной скорости
, где
- угловая скорость обращения. Поскольку радиус
станет меньше, то и линейная скорость станет меньше.
Ответ – 2
Б) Частота с периодом связана следующей формулой , поскольку период обращения не изменился, то и частота
обращения не изменилась. Ответ – 3



