Тема 12. Установление соответствия. Изменение величин

12.01 Кинематика

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела установление соответствия. изменение величин

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#73674

На покоящееся тело, находящееся на гладкой горизонтальной плоскости, в момент времени t = 0 начинают действовать две горизонтальные силы (см. рис.). Определите, как после этого изменяются со временем модуль скорости тела и модуль ускорения тела.

$PIC$

Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.

|--------------|----------------| |Модуль скорости|М-одуль ускорения| ---------------------------------

Источники: Банк ФИПИ

Показать ответ и решение

По второму закону Ньютона:

∑ ⃗Fi = F = m⃗a

где $Fi$ – сила, $m$ – масса тела, $a$ – ускорение тела, $F$ – равнодействующая сила.
В данном случае равнодействующая сила равна:

⃗F2+ F⃗1 =F2 − F1 = 2 Н

Так как сила постоянна, то и ускорение будет постоянно.
Скорость равна:

v = v0 +at,

где $v0$ – начальная скорость.
То есть модуль скорости тоже будет увеличиваться.

Ответ: 13

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#35381

Координата тела, движущегося вдоль оси Ох, изменяется по формуле:

2 x = 10 + 20t − 2t (единиц ы СИ)

Как меняются модуль ускорения и модуль скорости автомобиля в течение первых пяти секунд от начала движения?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется

|-----------------|----------------| |М-одуль-ускорения-|М-одуль-скорости-| ------------------------------------

Источники: Камзеева 2024

Показать ответ и решение

Общая формула перемещения тела записывается в виде:

at2- x = x0 + v0t + 2 ,

где $v0$ – начальная скорость, $t$ – время, $a$ – ускорение.
Отсюда ускорение равно $a = − 4 м/с2.$ Скорость будет описываться уравнением:

v = v0 + at = 20− 4t = 20 − 4⋅5 = 0.

То есть ускорение постоянно, а модуль скорости уменьшается.

Ответ: 32

Ошибка.
Попробуйте повторить позже

Задача 3#35380

Координата тела, движущегося вдоль оси Ох, изменяется по формуле:

x = 10− 4t− 2t2 (единицы СИ )

Как меняются модуль ускорения и модуль скорости автомобиля с течением времени?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется

|-----------------|----------------| |М-одуль-ускорения-|М-одуль-скорости-| ------------------------------------

Источники: Камзеева 2024

Показать ответ и решение

Общая формула перемещения тела записывается в виде:

at2- x = x0 + v0t + 2 ,

v = v0 + at = − 4− 4t.

То есть ускорение постоянно, а модуль скорости увеличивается.

Ответ: 31

Ошибка.
Попробуйте повторить позже

Задача 4#21836

На равномерно вращающемся диске жук переместился из точки А в точку В (см. рисунок). Как при этом изменились линейная скорость жука и частота его обращения вокруг оси O?

$PIC$

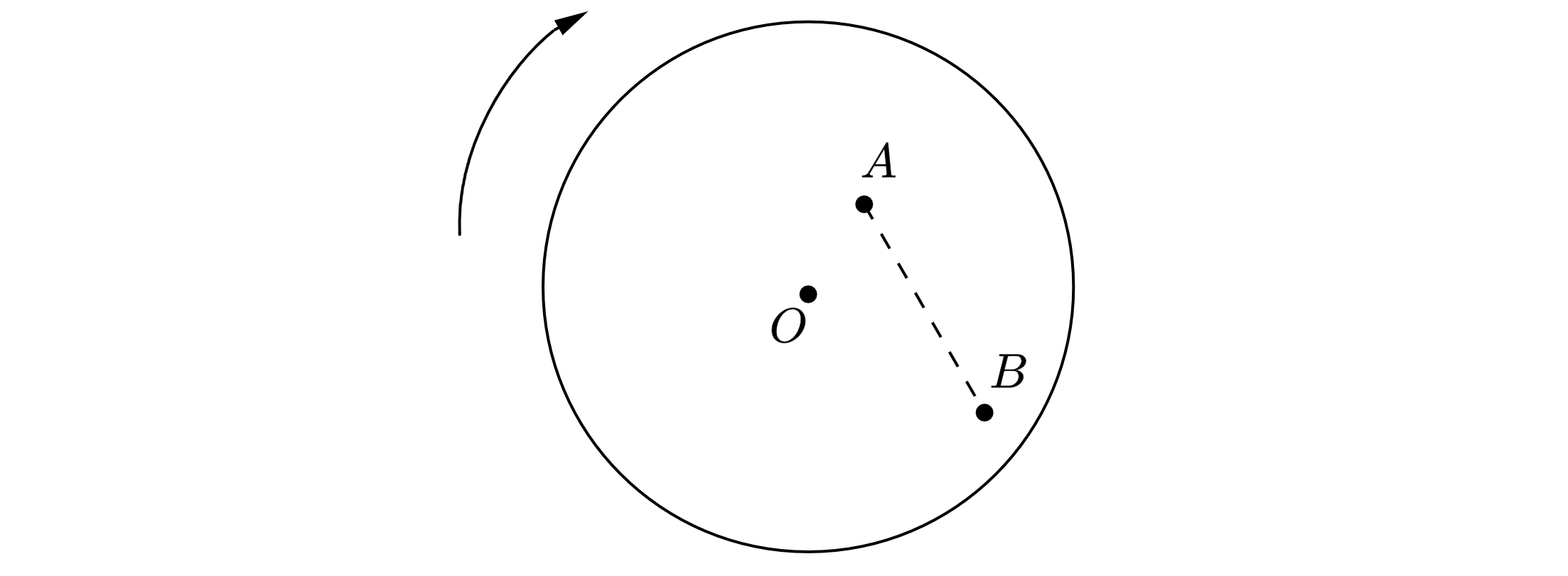
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

|---------------------|---------------------| |Л-иней-ная-скоро-сть-|Ч-астота-обращ-ени-я-| | | | --------------------------------------------

Источники: Банк ФИПИ

Показать ответ и решение

Угловая скорость диска постоянна для любых его точек. Линейная скорость равна:

v = ωR,

значит, при увеличении $R$ увеличивается и скорость.
Частота равна:

ω-- ν = 2π,

так как $ω = const$ , то $ν = const$

Ответ: 13

Ошибка.
Попробуйте повторить позже

Задача 5#73668

Муха сидела на равномерно вращающемся диске в точке А, а затем перелетела в точку В и села там (см. рисунок). Как в результате этого перемещения изменились линейная скорость мухи и частота её обращения на диске вокруг оси О?

$PIC$

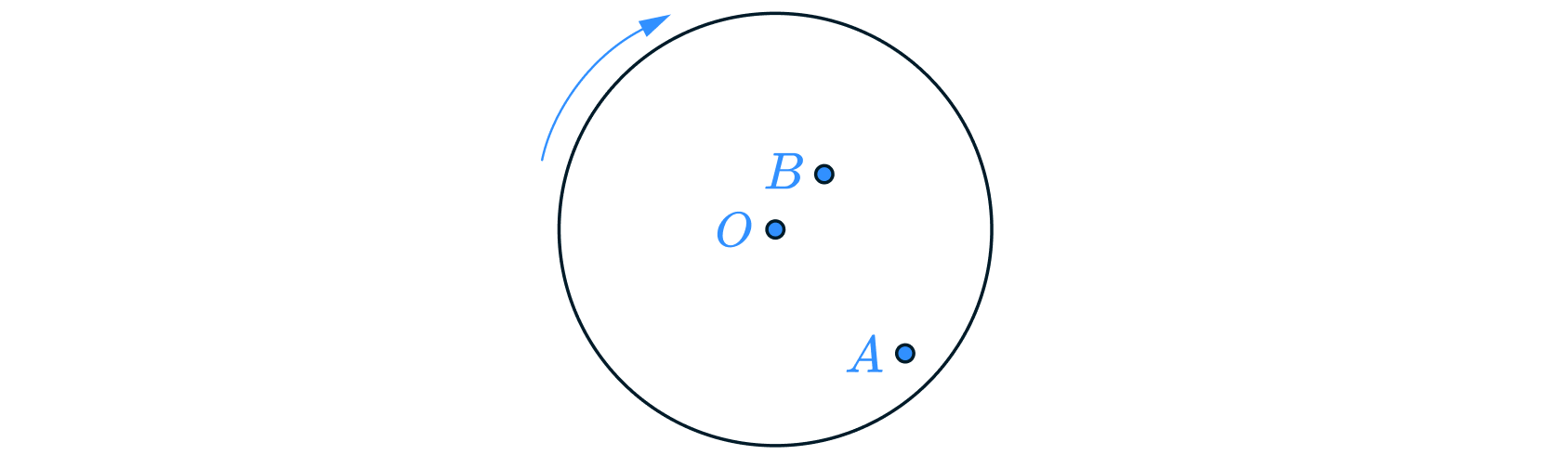
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится

|Линейная скорость-|Частота-обращ-ения-| | | | |------мухи-------|------мухи-------| -------------------------------------

Источники: Банк ФИПИ

Показать ответ и решение

А) При перемещении из точки $A$ в точку $B$ уменьшается радиус обращения мухи относительно точки $O$ . Поскольку период обращения диска не изменяется, то не изменяется и угловая скорость вращения диска. Формула для нахождения линейной скорости $v = ω⋅R$ , где $ω$ - угловая скорость обращения. Поскольку радиус $R$ станет меньше, то и линейная скорость станет меньше. Ответ – 2

Б) Частота с периодом связана следующей формулой $ν = 1- T$ , поскольку период обращения не изменился, то и частота обращения не изменилась. Ответ – 3

Ответ: 23

Ошибка.
Попробуйте повторить позже

Задача 6#37410

Брусок, лежащий на поверхности равномерно вращающегося горизонтально расположенного диска, переместили ближе к оси вращения диска. Как при этом изменились частота обращения бруска и модуль его центростремительного ускорения?
1) увеличилась
2) уменьшилась
3) не изменилась

|------------------|--------------------------------------| |Ч-астота-обращения-|М-одуль-цен-тр-остреми-тельного-ускорени-я-| | | | ----------------------------------------------------------

Источники: Камзеева 2024

Показать ответ и решение

Угловая скорость движения диска постоянна на всем протяжении диска, она равна:

v- ω = R .

Значит, при уменьшении радиуса движения $R$ во столько же раз уменьшается линейная скорость $v$ . Частота равна:

ν =-ω-, 2π

так как $ω = const$ , то и частота постоянна.
Центростремительное ускорение равно:

v2 2 a =-R = ω R,

так как $R$ уменьшается, то и уменьшается и центростремительное ускорение.

Ответ: 32

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#73673

На равномерно вращающемся диске жук переместился из точки $B$ в точку $A$ (см. рисунок). Как при этом изменились линейная скорость жука и частота его обращения вокруг оси $O$ ?

$PIC$

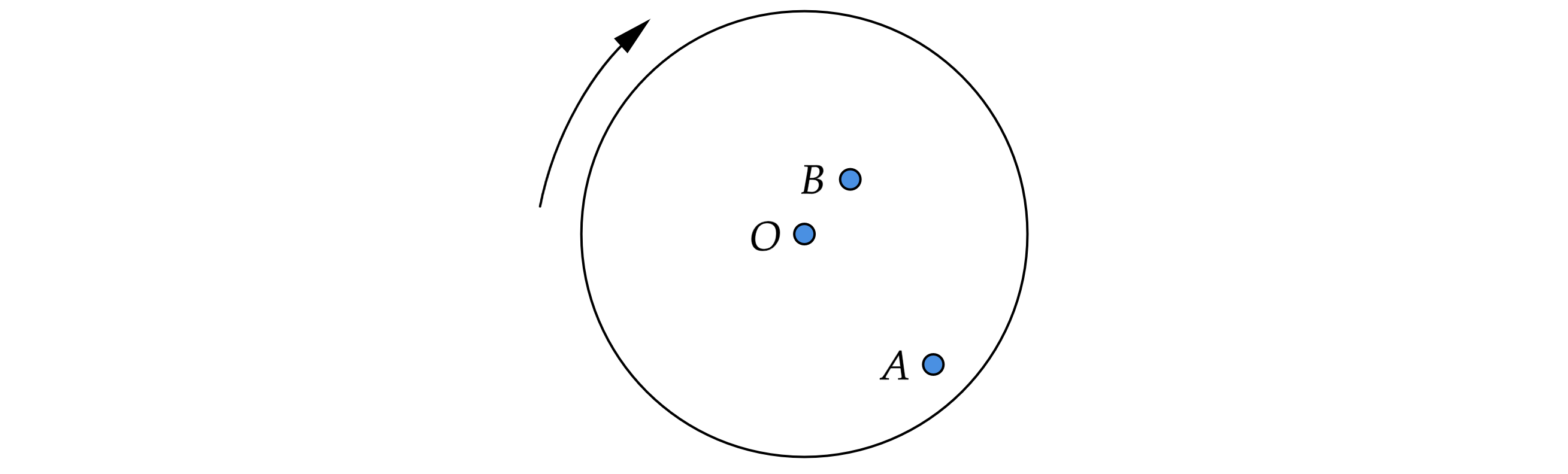
Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

|-----------------|-----------------| |Линейная скорость |Частота обращ ения | |------жука-------|------ж-ука-------| | | | -------------------------------------

Банк ФИПИ

Показать ответ и решение

А) При перемещении из точки $B$ в точку $A$ увеличивается радиус обращения жука относительно точки $O$ . Поскольку период обращения диска не изменяется, то не изменяется и угловая скорость вращения диска. Формула для нахождения линейной скорости $v = ω⋅R$ , где $ω$ - угловая скорость обращения. Поскольку радиус $R$ станет больше, то и линейная скорость станет больше. Ответ – 1

Ответ: 13

Ошибка.
Попробуйте повторить позже

Задача 8#73670

Космический корабль, движущийся по круговой орбите вокруг Земли, сместился на другую круговую орбиту, большего радиуса. Как при этом изменились сила тяготения, действующая на корабль со стороны Земли, и период обращения корабля вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится

|--------------|------------------------| |Сила-тяготения-|Период обращения-корабля-| ----------------------------------------|

Источники: Банк ФИПИ

Показать ответ и решение

А) Сила тяготения имеет формулу $GMm-- F = R2$ . Поскольку массы не изменились, а $G$ - константа, то при увеличении радиуса обращения сила тяготения будет уменьшаться. Ответ – 2

Б) Период обращения имеет формулу $T = 2πR- v$ , где $∘ ---- v = GM-- R$ - линейная скорость движения по орбите. Подставим в формулу периода и получим формулу $√--3 T = 2√π-R-- GM$ .Значит, при увеличении радиуса период тоже увеличится. Ответ – 1

Ответ: 21

Ошибка.
Попробуйте повторить позже

Задача 9#73671

Космический корабль, движущийся по круговой орбите вокруг Земли, сместился на другую круговую орбиту, меньшего радиуса. Как изменились в результате этого перехода модуль скорости корабля и период его обращения вокруг Земли? Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

|----------------|------------------------| |Скорость корабля|Период обращения-корабля-| ------------------------------------------|

Банк ФИПИ

Показать ответ и решение

А) Скорость корабля можно найти по формуле $∘-GM- v = -R--$ , поскольку радиус окружности уменьшается, модуль скорости увеличивается. Ответ – 1

Б) Период обращения имеет формулу $T = 2πR- v$ , где $∘ ---- v = GM-- R$ - линейная скорость движения по орбите. Подставим в формулу периода и получим формулу $√--- T = 2√π-R3- GM$ .Значит, при уменьшении радиуса период тоже уменьшится. Ответ – 2

Ответ: 12

Ошибка.
Попробуйте повторить позже

Задача 10#104678

Жук сидит на равномерно вращающемся диске в точке А. Через некоторое время жук переместился в точку В (см. рисунок). Как при перемене положения изменяются линейная скорость жука и частота его вращения? Сопротивление воздуха не учитывать. Масса жука гораздо меньше массы диска.

$PIC$

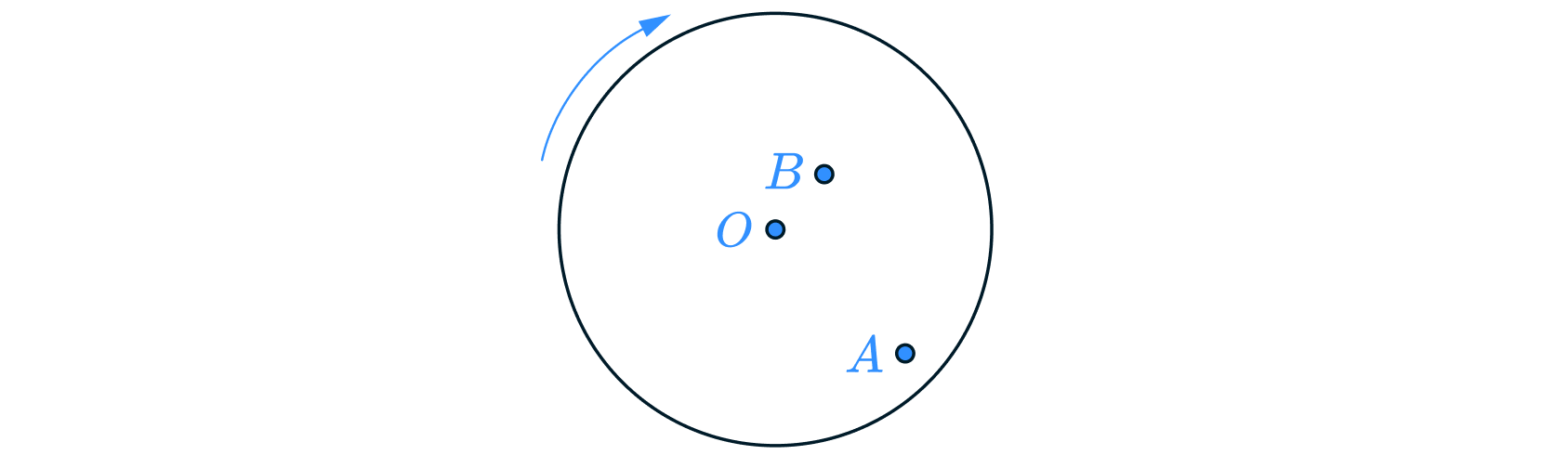
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.

|-----------------|-----------------| |Линейная скорость |Ч астота вращения | |------ж-ука------|------ж-ука-------| | | | ------------------------------------

Источники: Статград 2025 декабрь №1 ОГЭ

Показать ответ и решение

Ответ: 23

Ошибка.
Попробуйте повторить позже

Задача 11#104727

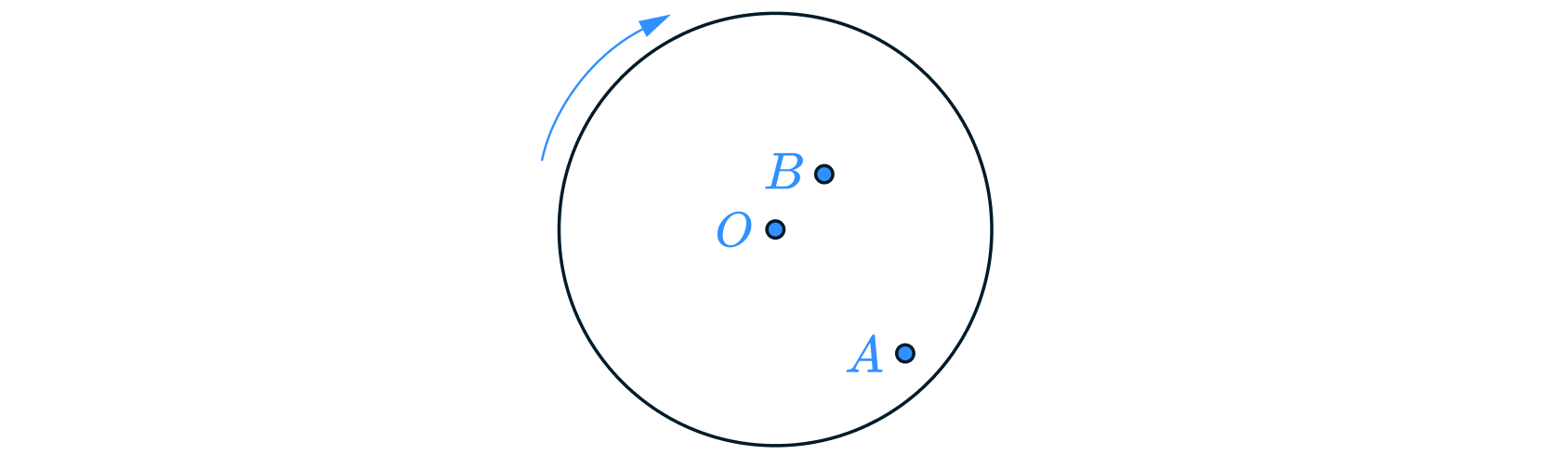
Жук сидит на равномерно вращающемся диске в точке А. Через некоторое время жук переместился в точку В (см. рисунок). Как при перемене положения изменяются период вращения жука и центростремительное ускорение жука? Сопротивление воздуха не учитывать. Масса жука гораздо меньше массы диска.

$PIC$

|---------------|-------------------| |Период вращ ения|Ц ентростремительно | |-----ж-ука-----|---ускорение ж-ука--| | | | ------------------------------------

Источники: Статград 2025 декабрь №2 ОГЭ

Показать ответ и решение

А) Поскольку период обращения диска не изменяется, то не изменяется и угловая скорость вращения диска. А значит не изменяется и период вращения жука. Ответ – 3

А) При перемещении из точки $A$ в точку $B$ уменьшается радиус обращения мухи относительно точки $O$ . Поскольку период обращения диска не изменяется, то не изменяется и угловая скорость вращения диска. Формула для нахождения линейной скорости $v = ω⋅R$ , где $ω$ - угловая скорость обращения. Центростремительное ускорение $v2 2 a = R-= ω R$ . Поскольку радиус $R$ станет меньше, то и центростремительное ускорение станет меньше. Ответ – 2

Ответ: 32