02 Динамика. Импульс. Закон сохранения импульса - Каталог заданий по ОГЭ

Ошибка.
Попробуйте повторить позже

Задача 1#111367

Тело массой 2 кг движется по окружности радиусом 2 м с постоянной по модулю скоростью 3 м/с. Чему равен модуль равнодействующей сил, приложенных к телу?

Источники: Банк ФИПИ | Камзеева 2024

Показать ответ и решение

Запишем второй закон Ньютона:

⃗ F = m ⃗a,

где $F$ – равнодействующая сила, $m$ – масса тела, $a$ – ускорение.
Так как движение происходит по окружности, то ускорение центростремительное:

v2 a =-R ,

где $v$ – скорость, $R$ – радиус окружности.
Тогда

F = m v2 = 2 к г9 (м/с)2= 9 Н R 2 м

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 2#74161

Самолёт совершает «мёртвую петлю». Чему равен радиус петли, если лётчик в верхней точке петли оказывается в состоянии невесомости при скорости 100 м/с?

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

Состояние невесомости это такой момент времени, когда вес тела равен нулю, то есть нет соприкосновения с опорой, а значит и сила реакции опоры равна нулю. В наивысшей точки траектории при движении по окружности центростремительное ускорение направлено вертикально вниз и сила тяжести направлена вертикально вниз. Тогда по второму закону Ньютона в проекции на вертикальную ось получим:

ma = mg

a= g

Ускорение $2 a= v- R$ Получим:

v2 = g R

Откуда радиус равен :

v2 R = g-

Считаем:

R = 1002= 1000 м 10

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: второй закон Ньютона, формула центростремительного ускорения)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 3#37423

С какой скоростью должен лететь самолёт в наивысшей точке «мёртвой петли» радиусом 1 км, чтобы лётчик оказался в невесомости?

Источники: Банк ФИПИ | Камзеева 2024

Показать ответ и решение

$PIC$

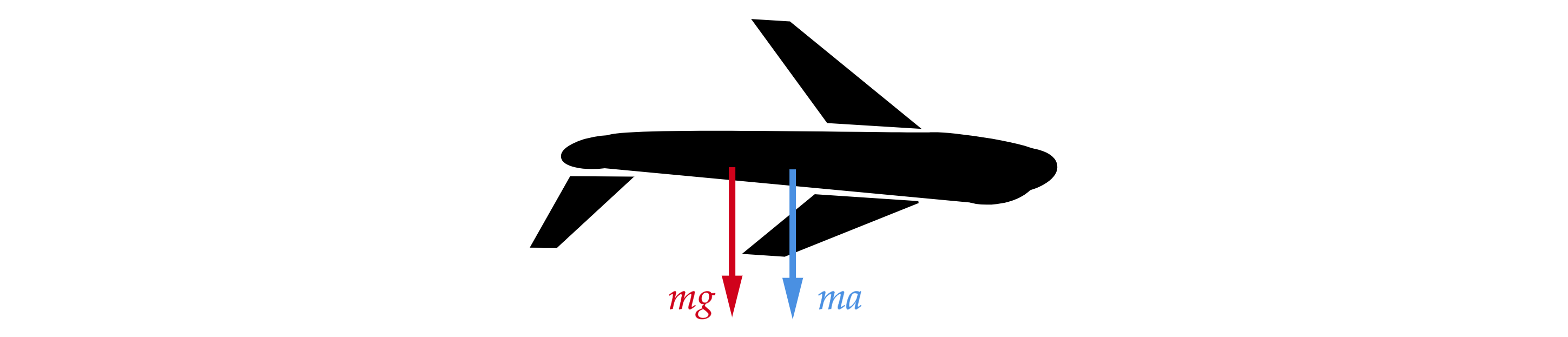
Состояние невесомости это такой момент времени, когда вес тела равен нулю, то есть нет соприкосновения с опорой, а значит и сила реакции опоры равна нулю. В наивысшей точки траектории при движении по окружности центростремительное ускорение направлено вертикально вниз и сила тяжести направлена вертикально вниз. Тогда по второму закону Ньютона в проекции на вертикальную ось получим:

ma = mg

a = g

Ускорение $2 a = v- R$ Получим:

2 v- = g R

Откуда скорость равна:

∘--- v = gR

Считаем:

v = √10-⋅1000 = 100 м/ с

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула центростремительного ускорения, описано состояние невесомости, формула силы тяжести)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 4#74166

Тело движется вдоль оси $OX.$ Проекция на эту ось равнодействующей всех сил, приложенных к телу, равна $3 Н.$ В таблице приведена зависимость проекции скорости $vx$ этого тела от времени $t.$ Чему равна масса тела?

|-------|--|-|--|---|---| |-t, с--|2-|4|-6|-8-|10-| -vx, м/с-3--6--9-12--15--

Источники: Банк ФИПИ

Показать ответ и решение

Приложенная к телу сила создает у тела ускорение.

Связь между силой и ускорением описывается формулой $F = ma$ , откуда масса равна $m = F- a$

Ускорение тела рассчитывается по формуле $a= vx−-v0x t$

Тогда масса равна $F t m = vx−-v0x-$

Считаем:

m = 3-⋅(6−-2)= 2 кг 9− 3

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула связи силы и ускорения, формула ускорения)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 5#74164

Брусок массой 100 г, подвешенный на легкой нити, поднимают вертикально вверх с ускорением, равным по модулю 1 м/с² и направленным вверх. Чему равен модуль силы натяжения нити?

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

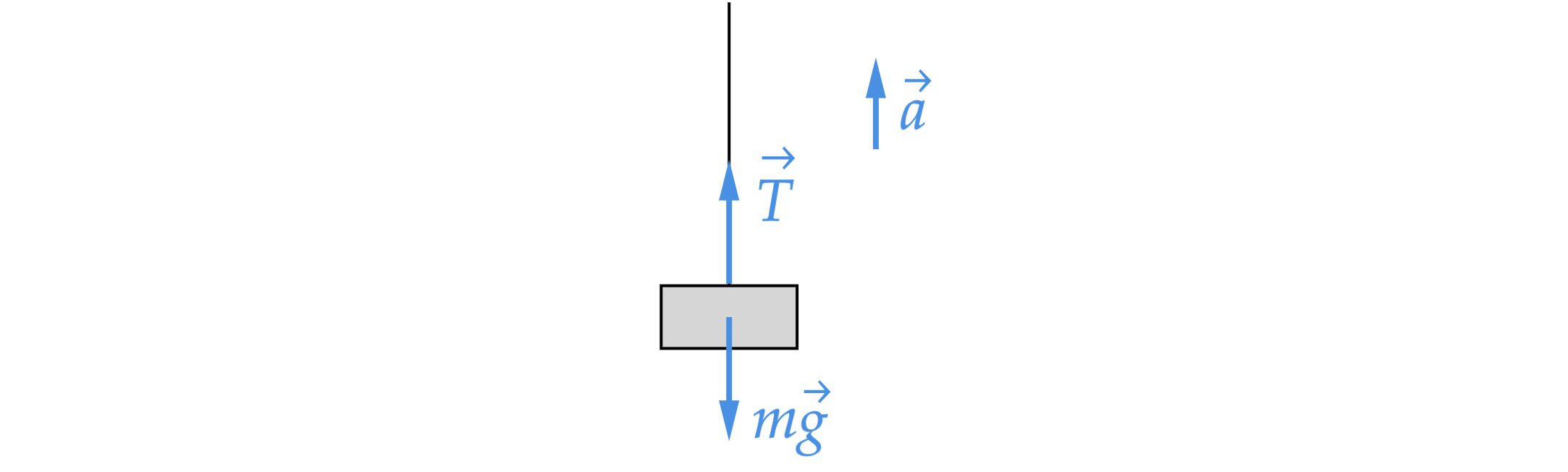
При движении вверх с ускорением, для тела можно применить второй закон Ньютона относительно Земли. Запишем его в проекции на вертикальную ось

ma= T − mg

здесь $T$ - сила натяжения нити. Выразим её:

T = m (a + g)

Посчитаем:

T = 0,1⋅(1+ 10)= 1,1 Н

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: второй закон Ньютона, формула силы тяжести)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 6#74167

Брусок массой 100 г покоится на горизонтальной поверхности. Какую силу, направленную горизонтально, нужно приложить к бруску, чтобы он мог двигаться с ускорением $2 м∕с2$ ? Коэффициент трения между бруском и поверхностью равен 0,1.

Источники: Банк ФИПИ | Камзеева 2024

Показать ответ и решение

$PIC$

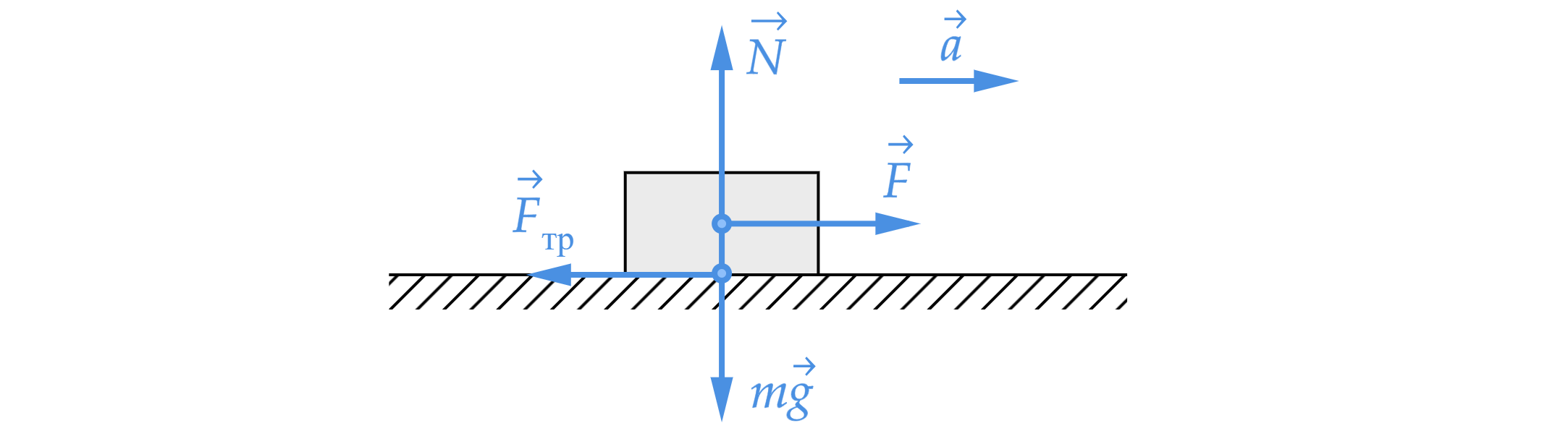
Запишем второй закон Ньютона в проекции на вертикальную и горизонтальную ось:

OY :0 = N − mg

OX :ma = F − Fтр

Из оси $OY$ получаем $N = mg$ .
Поскольку тело движется, сила трения равняется максимально возможной силе трения и находится по формуле $F тр = μN = μmg$ Подставим все в уравнение $OX$ , получим:

ma = F − μmg

Выразим силу $F$ :

F = ma +μmg

F = m(a+ μg)

F = 0,1(2 +0,1⋅10)= 0,3 Н

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: второй закон Ньютона, формула силы трения скольжения, формула силы тяжести)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 7#74165

Коробку массой 10 кг равномерно и прямолинейно тянут по горизонтальной поверхности с помощью горизонтальной пружины жёсткостью 200 Н/м. Удлинение пружины 0,2 м. Чему равен коэффициент трения?

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

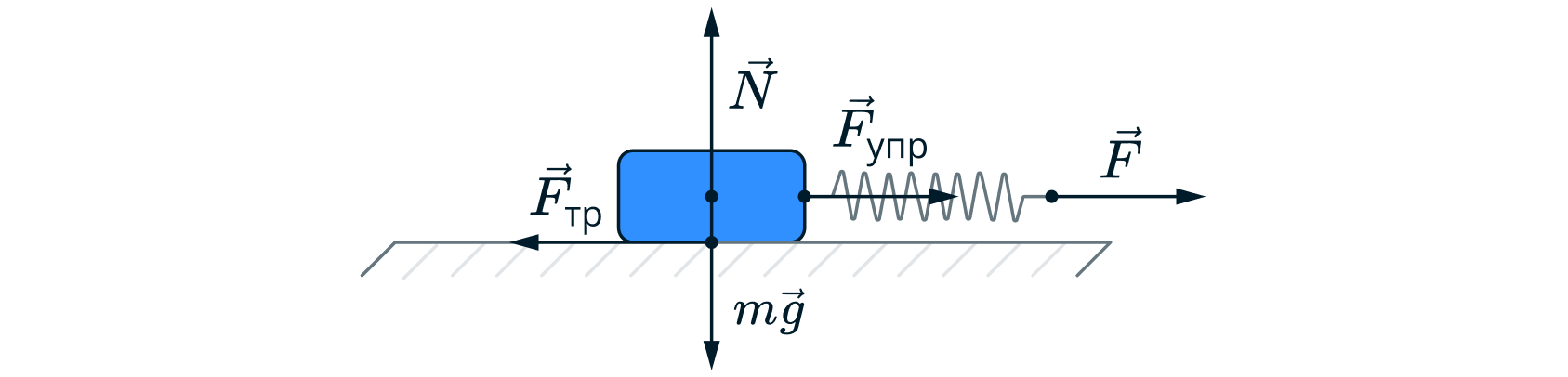
Тело тянут равномерно, значит ускорение у тела отсутствует. Запишем второй закон Ньютона для тела в проекции на вертикальную и горизонтальную ось:

OY :0 = N − mg

OX :0 = Fупр− Fтр

Поскольку тело движется, то сила трения равняется максимально возможной силе трения, т.е. силе трения скольжения и находится по формуле $Fтр = μ ⋅N$

Из уравнения вертикальной оси получаем $N = mg$ , значит, сила трения равна $Fтр = μmg$ .

Сила упругости по закону Гука в свою очередь равна $Fупр =kΔx$ .

Из уравнения горизонтальной оси получим:

Fтр = Fупр

μmg = kΔx

Откуда коэффициент трения равен:

kΔx μ = mg--

Считаем:

μ = 200⋅0,2-= 0,4 10⋅10

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: второй закон Ньютона, закон Гука (формула силы упругости), формула силы трения скольжения, формула силы тяжести, сказано чему равно ускорение)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 8#74163

Однородный стержень (см. рисунок) подвешен на двух одинаковых вертикальных пружинах жёсткостью 800 Н/м каждая. Какова масса стержня, если удлинение каждой пружины равно 2 см? Стержень неподвижен.

$PIC$

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

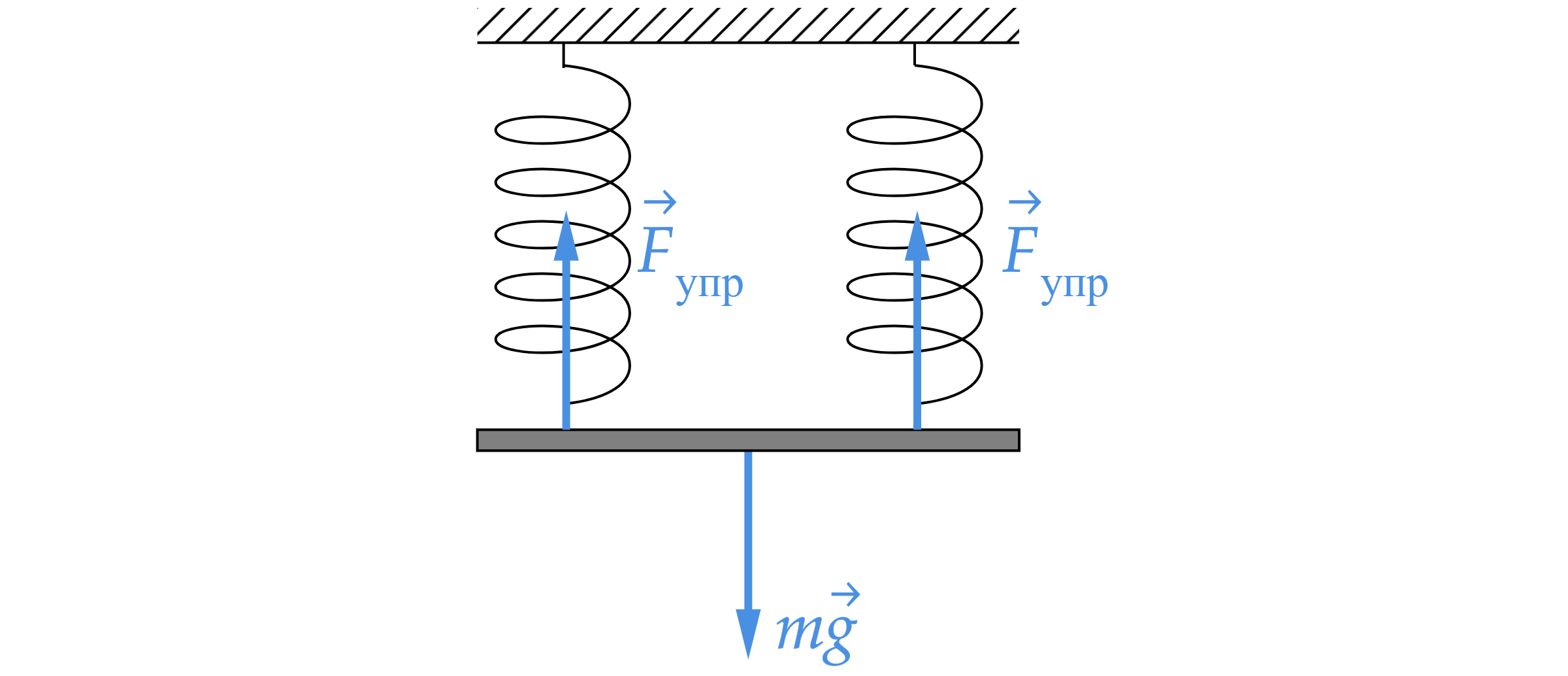
Стержень неподвижен, а пружины вертикальны и растянуты на одно и то же значение. Из этого можно сделать вывод, что ускорение тела равно нулю, а сила упругости, со стороны каждой из пружинок находится по закону Гука по формуле $Fупр = kΔx$ Так как ускорение равно нулю, то из второго закона Ньютона в проекции на вертикальную ось получаем:

F упр+ Fупр− mg =0

2Fупр − mg = 0

2kΔx = mg

Тогда масса стержня равна:

2kΔx m = -g---

Считаем:

M = 2⋅800⋅0,02-= 3,2 кг 10

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: второй закон Ньютона, закон Гука (формула силы упругости), формула силы тяжести)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 9#74168

Однородный стержень массой 2 кг (см. рисунок) подвешен на двух одинаковых невесомых вертикальных пружинках. Какова жесткость каждой пружины, если удлинение каждой пружины равно 2 см? стержень неподвижен

$PIC$

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

Стержень неподвижен, а пружины вертикальны и растянуты на одно и то же значение. Из этого можно сделать вывод, что ускорение тела равно нулю, а сила упругости, со стороны каждой из пружинок находится по закону Гука по формуле $Fупр = kΔx$ Так как ускорение равно нулю, то из второго закона Ньютона в проекции на вертикальную ось получаем:

F упр+ Fупр− mg =0

2Fупр − mg = 0

2kΔx = mg

Тогда жесткость пружин равна:

mg k = 2Δx-

Считаем:

k =-2⋅10- =500 Н/м 2 ⋅0,02

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: второй закон Ньютона, закон Гука (формула силы упругости), формула силы тяжести)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 10#52762

Конькобежец массой 60 кг, стоя на коньках на льду, бросает вперёд в горизонтальном направлении предмет массой 1 кг и откатывается назад на 40 см. Коэффициент трения коньков о лёд 0,02. Найдите скорость, с которой был брошен предмет.

Источники: Банк ФИПИ | Камзеева 2024

Показать ответ и решение

$PIC$

Запишем закон сохранения импульса:

0 =M ⃗v +m ⃗u,

где $M$ – масса человека, $v$ – его скорость после броска, $m$ – масса предмета, $u$ – его скорость после броска.
Спроецируем на горизонтальную ось

M Mv = mu ⇒ u= vm-.

Движение конькобежца по льду можно описать вторым законом Ньютона:

F⃗тр+ N⃗+ M ⃗g = M ⃗a,

где $Fтр$ – сила трения скольжения, $a$ – его ускорение, $N$ - сила реакции опоры.
Спроецировав на вертикальную ось получим:

N = mg

По закону Амонтона-Кулона:

Fтр = μN

Тогда сила трения скольжения равна:

Fтр = μMg,

где $μ$ – коэффициент трения скольжения.
Тогда, спроецировав второй закон Ньютона на горизонтальную ось

μMg = Ma ⇒ a= μg.

То есть движение конькобежца равнозамедленное. Расстояние, которое пройдёт конькобежец равно:

2 2 S = v-= -v-. 2a 2μg

Отсюда выразим начальную скорость

v =∘2-μgS.

И подставив в первое уравнение

u= M-∘2-μgS-= 60 кг∘2-⋅0,02-⋅10 Н/кг⋅0,4 м-= 24 м/с m 1 кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: второй закон Ньютона, закон сохранения импульса, формула импульса, формула силы трения скольжения, формула пути при равноускоренном движении)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 11#74169

Конькобежец массой 60 кг, стоя на коньках на льду, бросает в горизонтальном направлении предмет массой 1 кг со скоростью 24 м/с и откатывается на 40 см. Найдите коэффициент трения коньков о лёд.

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

Поскольку система предмет+конькобежец является замкнутой и на систему не действуют никакие внешние силы в горизонтальном направлении, то в горизонтальном направлении выполняется закон сохранения импульса. Запишем закон сохранения импульса в проекции на горизонтальную ось:

0 =p⃗к +⃗pш

0 = MU − mv

Здесь $pк = MU$ - импульс конькобежца, $pш = mv$ - импульс шайбы.
Выразим отсюда скорость конькобежца:

U = mv- M

Сказано, что конькобежец откатывается на 40 см, значит, в конце он останавливается - его скорость равна 0. Человек останавливается, так как он движется с замедляющим ускорением, которое вызвано силой трения. тогда получим:

Ma = Fтр

Поскольку тело движется, то сила трения равняется максимально возможной силе, рассчитываемой по формуле $Fтр = μN$ , при этом $N =Mg$ , а значит, $F тр =μMg$ В итоге получаем:

Ma = μMg

a = μg

Запишем формулу для нахождения пути:

0− U2 U2 S = -−2a-= 2a-

Получаем:

(mv)2 S = 2M2μg-

Откуда коэффициент трения:

μ = (mv)2- 2SgM2

(1 ⋅24)2 μ = 2⋅0,4⋅10⋅602 = 0,02

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула импульса, закон сохранения импульса, второй закон Ньютона, формула силы трения скольжения, формула пути при равноускоренном движении тела)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 12#74310

Конькобежец массой 80 кг, стоя на коньках на льду, бросает в горизонтальном направлении предмет со скоростью 20 м/с и откатывается в обратном направлении на 40 см. Найдите массу предмета, если коэффициент трения коньков о лёд равен 0,02.

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

Момент броска можно описать законом сохранения импульса:

0 = MU − mv

$M$ - масса конькобежца, $m$ - масса предмета, $v$ - скорость предмета, $U$ - скорость отката конькобежца. Из закона сохранения импульса найдем скорость конькобежца:

mv U = M--

При откате на конькобежца действует сила трения, которая вызывает ускорение, за счет которого его скорость уменьшается до 0. Расстояние отката можно найти по формуле:

S = U2к −-U2 −2a

$Uк$ - конечная скорость конькобежца, равная 0, перед ускорением стоит минус, поскольку ускорение направлено противоположно направлению скорости.

U2 S = 2a-

2 S = (mv) 2aM2

Запишем второй закон Ньютона для конькобежца:

⃗ ⃗ M⃗a = M ⃗g+ N +F тр

Спроецируем на вертикальную и горизонтальную ось:

OX :Ma = Fтр

OY :0= N − Mg

Поскольку конькобежец движется, сила трения равна максимально возможной силе трения и равна $μN$ . Из уравнения оси $OY$ получаем $N =Mg$ , тогда сила трения равна $μMg$ Из уравнения оси $OX$ получим:

Ma = μMg

a = μg

Тогда получим:

(mv)2 S = 2μgM2-

Отсюда масса предмета равна:

∘ ------2- m = 2SμgM2-- v

∘ ----------------- 2⋅0,4⋅0,02-⋅10⋅802- m = 202 = 1,6 кг

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: второй закон Ньютона, формула импульса, закон сохранения импульса, формула пути при равноускоренном движении)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 13#37421

Вагон массой 20 т, движущийся по горизонтальному пути со скоростью 2 м/с, сталкивается с другим вагоном такой же массы, движущимся ему навстречу со скоростью 1 м/с, и автоматически с ним сцепляется. С каким ускорением будут двигаться вагоны после сцепки, если они пройдут до полной остановки 25 м?

Источники: Банк ФИПИ | Камзеева 2024

Показать ответ и решение

$PIC$

Запишем закон сохранения импульса при соударении вагонов:

p⃗1 +p⃗2 = ⃗p

m ⃗v1+ mv⃗2 = (m + m)⃗v,

где $p= mv$ - формула расчёта импульса, $m$ – масса вагонов, $v1$ и $v2$ – скорости вагонов до соударения, $v$ – скорость вагонов после сцепки.
Спроецируем на ось, совпадающую с осью удара:

mv1 − mv2 = (m + m)v.

Отсюда

v = v1-− v2-= 2 м/с-− 1-м/с= 0,5 м/с. 2 2

После движение происходит с постоянным ускорением. Запишем формулы кинематики:

S = vt− at2, 2

где $a$ – ускорение, $t$ – время движения.
Так как конечная скорость равна нулю, то

0= v− at

Тогда

v t= a

Отсюда

2 2 2 S = v- ⇒ a= -v-= 0,25 (м/с)-= 0,005 м/с2 2a 2S 2⋅25 м

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула импульса, закон сохранения импульса, формула пути при равноускоренном движении)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 14#74153

Вагон массой 20 т, движущийся по горизонтальному пути со скоростью 2 м/с, сталкивается с другим вагоном такой же массы, движущимся ему навстречу со скоростью 1 м/с, и автоматически с ним сцепляется. Какой путь они пройдут до полной остановки, если будут двигаться после сцепки с ускорением $0,005 м/с2$ ?

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

Процесс сталкивания и сцепления вагонов можно считать мгновенным, значит, его можно описывать законом сохранения импульса в проекции на горизонтальную ось:

p1 − p2 = p

$p1 = mv1$ - импульс первого вагона, $p2 =mv2$ - импульс второго вагона, $p= (m + m)v$ - импульс вагонов после сцепления Получим:

mv1− mv2 = (m + m)v

Откуда скорость после сцепления:

v = m-(v1−-v2)= v1−-v2 m +m 2

После сцепления вагоны движутся до остановки, значит, конечная скорость их совместного движения равна 0. Тогда путь можно будет рассчитать по формуле $v2к− v2 S = -−2a--$ , при этом, перед ускорением стоит знак минус, поскольку оно направлено противоположно движению, $vк = 0$ , так как вагоны останавливаются. Получим:

v2 S = 2a

Подставим формулу для $v$ :

2 S = (v1-− v2)-= 25 м 8a

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула импульса, закон сохранения импульса, формула пути при равноускоренном движении)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 15#74300

Брусок массой 1,8 кг движется со скоростью 2 м/с по гладкой горизонтальной поверхности. Навстречу бруску летит пуля массой 9 г, которая пробивает брусок насквозь и вылетает из него со скоростью 500 м/с. При этом брусок останавливается. Чему равна скорость пули до встречи с бруском?

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

Запишем процесс взаимодействия пули и бруска, этот процесс можно считать мгновенным, значит, выполняется закон сохранения импульса для системы тел в проекции на горизонтальную ось:

mv1− Mv2 = mv3

Здесь $m$ - масса пули, $M$ - масса бруска, $v1$ - скорость пули до соударения, $v2$ - скорость бруска до соударения, $v3$ - скорость пули после вылета из бруска.
Отсюда скорость пули до соударения равна:

v1 = mv3-+-Mv2 m

9-⋅10−3-⋅500+-1,8⋅2 v1 = 9⋅10−3 = 900 м/с

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула импульса, закон сохранения импульса)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 16#74302

Снаряд, движущийся горизонтально, разорвался на два равных осколка по 1 кг каждый. Один осколок продолжил двигаться относительно Земли в прежнем направлении со скоростью 800 м/с, а другой полетел назад со скоростью 400 м/с. Какую скорость имел снаряд в момент разрыва?

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

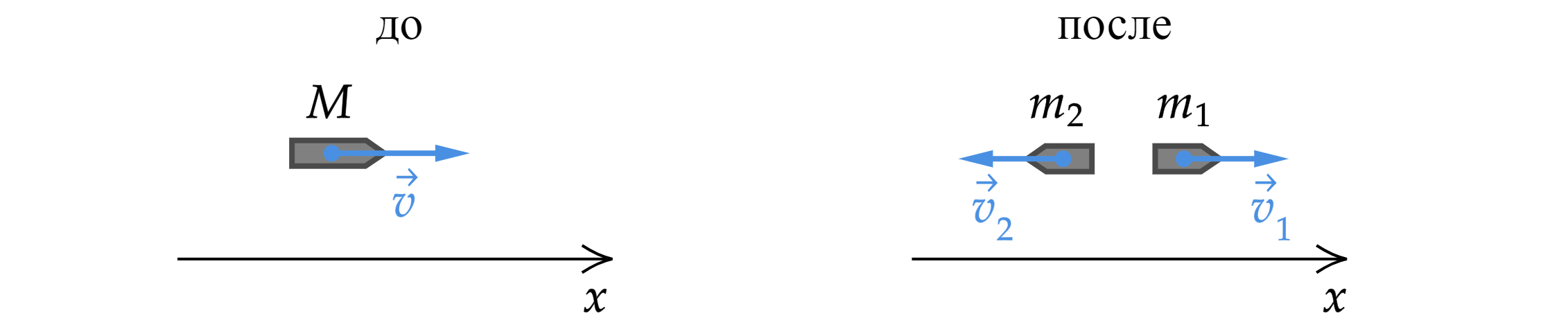
Процесс разрыва можно считать мгновенным, а значит, выполняется закон сохранения импульса в проекции на горизонтальную ось:

Mv =m1v1 − m2v2

Здесь $M$ - исходная масса снаряда, при этом $M m1 = m2 = 2-$ Получим:

M M Mv = 2-v1− 2-v2

2v = v1− v2

Значит скорость $v$ в момент разрыва:

v = v1−-v2- 2

v = 800-− 400-= 200 м/с 2

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула импульса, закон сохранения импульса)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 17#74301

Тело массой 800 г движется в горизонтальном направлении со скоростью 4 м/с и сталкивается с телом массой 400 г, движущимся по той же прямой ему навстречу со скоростью 2 м/с. Определите скорость тел после удара, если они стали двигаться как единое целое.

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

Запишем процесс взаимодействия тел, этот процесс можно считать мгновенным, значит, выполняется закон сохранения импульса для системы тел в проекции на горизонтальную ось:

mv1 − Mv2 = (m + M )v

Здесь $m = 800$ г - масса первого тела, обладающего скоростью $v1 =4$ м/с, $M = 400$ г - масса второго тела, обладающего скоростью $v2 = 2$ м/с, $v$ - искомая скорость тел, после соударения.
Выразим искомую скорость и посчитаем ее:

v = mv1-− Mv2 m +M

800⋅4− 400⋅2 v =--800+-400-- = 2 м/с

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формула импульса, закон сохранения импульса)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 18#37416

Искусственный спутник движется вокруг Луны по круговой орбите на расстоянии 100 км от поверхности Луны. Чему равна орбитальная скорость спутника? Масса Луны равна $7,3 ⋅1022 кг,$ радиус – $1,7⋅106 м.$

Источники: Камзеева 2024

Показать ответ и решение

При движении на спутник действует центростремительное ускорение, равное:

v2 a= -R,

где $v$ – скорость спутника, $R$ – радиус орбиты.
По второму закону Ньютона:

F = ma,

в данном случае $F$ – сила тяготения, $m$ – масса спутника.
Сила тяготения равна:

F = GmM--, R2

где $M$ – масса Луны Тогда

2 ∘---- G mM2-= m v-⇒ v = GM-. R R R

Радиус орбиты равен радиусы Луны + 100 км, тогда

-------------- ∘ GM v = Rлуны+-100⋅103 ≈ 1645 м/c

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: закон Всемирного тяготения, второй закон Ньютона, формула центростремительного ускорения)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 19#37422

Какой путь пройдёт машина на горизонтальном участке дороги после выключения двигателя, если коэффициент трения составляет 0,2, а скорость движения машины 72 км/ч?

Источники: Камзеева 2024

Показать ответ и решение

Запишем второй закон Ньютона для бруска:

⃗ ⃗ Fтр + N + m ⃗g = m⃗a,

где $F тр$ – препятствующая сила трения, $m$ – масса бруска, $a$ – ускорение, $N$ – сила реакции опоры.
Спроецируем второй закон Ньютона на ось, совпадающую с осью движения бруска:

Fтр = ma.

Сила трения скольжения равна:

F тр = μN = μmg,

Тогда

μmg = ma ⇒ a = μg

Запишем формулы кинематики:

2 S = vt− at-, 2

где $a$ – ускорение, $t$ – время движения.
Так как конечная скорость равна нулю, то

0 = v − at

Тогда

v- t = a

Отсюда

v2 -v2- --400-(м/-с)2-- S = 2a = 2μg = 2 ⋅0,2 ⋅10 м/с2 = 100 м

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: второй закон Ньютона в векторном виде и в проекции на выбранные координатные оси, формула силы тяжести, формула силы трения, формулы кинематики равноускоренного движения)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 20#43921

Поезд, масса которого 4000 т, движущийся со скоростью 36 км/ч, начал торможение. За 1 минуту поезд проехал 510 м. Чему равна сила трения, действующая на поезд?

Источники: Камзеева 2024

Показать ответ и решение

Запишем второй закон Ньютона для автомобиля:

⃗ ⃗ Fтр + N + m ⃗g = m⃗a,

где $F тр$ – препятствующая сила трения, $m$ – масса бруска, $a$ – ускорение, $N$ – сила реакции опоры.
Спроецируем второй закон Ньютона на ось, совпадающую с осью движения бруска:

Fтр = ma.

Запишем формулы кинематики:

t2 S = v0t − a 2 ,

где $v0$ – начальная скорость, $a$ – ускорение, $t$ – время движения.
Определим ускорение автомобиля:

a = 2(v0t−-S) t2

Окончательно сила трения:

( 2(v0t−-S)) 6 ( 2(10 м/с-⋅60 с−-510-м)) 5 Fтр = m t2 = 4 ⋅10 кг 3600 с2 = 2⋅10 Н

Ответ:

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Представлено полное правильное решение, включающее следующие	3
элементы:
1) верно записано краткое условие задачи;
2) записаны уравнения и формулы, применение которых
необходимо и достаточно для решения задачи выбранным
спосбом (в данном решении: формулы кинематики равноускоренно движущегося тела, второй закон Ньютона в векторном виде и в проекции на выбранные координатные оси)

Правильно записаны необходимые формулы, проведены	2
вычисления и получен ответ (верный или неверный), но допущена
ошибка в записи краткого условия или переводе единиц в СИ
ИЛИ
Представлено правильное решение только в общем виде, без каких-
либо числовых расчётов
ИЛИ
Записаны уравнения и формулы, применение которых необходимо
и достаточно для решения задачи выбранным способом, но
в математических преобразованиях или вычислениях допущена
ошибка

Записано и использовано не менее половины исходных формул,	1
необходимых для решения задачи
ИЛИ
Записаны все исходные формулы, но в одной из них допущена
ошибка

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	3