22.02 Закон Джоуля-Ленца. КПД
Ошибка.
Попробуйте повторить позже
В электрическую сеть с напряжением 120 В включены пять резисторов по схеме, изображенной на рисунке. Сопротивления
резисторов равны: 
= 2 Ом, 
= 20 Ом, 
= 15 Ом, 
= 
= 10 Ом.
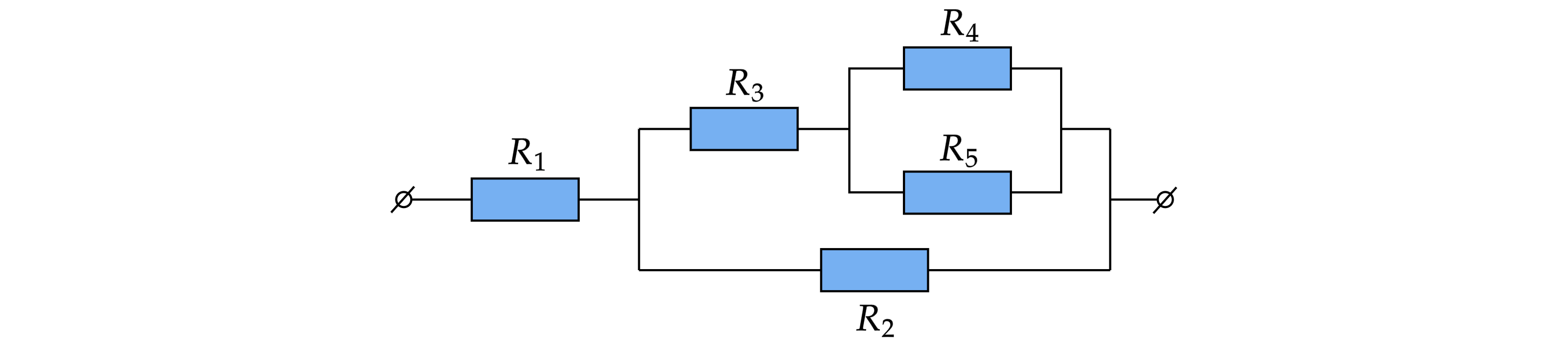
Определите мощность, потребляемую резистором 
.
Источники:
Вспомним, что при параллельном соединении резисторов 
, 
их общее сопротивление равно
Также понятно, что при соединении 
резисторов одного номинала 
общее сопротивление будет равно
При последовательном же соединении общее сопротивление является аддитивной величиной, то есть, их общее сопротивление
является суммой сопротивлений каждого отдельного резистора.
Рассчитаем общее сопротивление цепи: 
. Общий ток в цепи по закону Ома равен
Т.к. резисторы 2 и 3,4,5 соединены параллельно, причем их номиналы равны, то ток, попадающий в их узел, делится
пополам.
Тогда ток, текующий через резистор 3, равен 
.
Проводя аналогичные рассуждения для резисторов 4 и 5, получим, что ток, текущий через резистор 4, равен 
По закону
Джоуля-Ленца мощность на резисторе равна
Тогда мощность на резисторе 4 равна:
| Критерии оценивания выполнения задачи | Баллы |
| Представлено полное правильное решение, включающее следующие | 3 |
| элементы: | |
| 1) верно записано краткое условие задачи; | |
| 2) записаны уравнения и формулы, применение которых | |
| необходимо и достаточно для решения задачи выбранным | |
| спосбом (в данном решении: формула мощности, выделяющей в резистооре при протекании тока, законы последовательного и параллельного соединения резисторов, закон Ома) | |
| Правильно записаны необходимые формулы, проведены | 2 |
| вычисления и получен ответ (верный или неверный), но допущена | |
| ошибка в записи краткого условия или переводе единиц в СИ | |
|
ИЛИ
| |
| Представлено правильное решение только в общем виде, без каких- | |
| либо числовых расчётов | |
|
ИЛИ
| |
| Записаны уравнения и формулы, применение которых необходимо | |
| и достаточно для решения задачи выбранным способом, но | |
| в математических преобразованиях или вычислениях допущена | |
| ошибка | |
| Записано и использовано не менее половины исходных формул, | 1 |
| необходимых для решения задачи | |
|
ИЛИ
| |
| Записаны все исходные формулы, но в одной из них допущена | |
| ошибка | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 3 |
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
